Понятие логической переменной и логической функции. Основные логические соотношения и операции над одной и двумя переменными. Закон Де Моргана.
В 1847 году математик Дж. Буль создает алгебру двоичных переменных. Переменная в данной системе может принимать значение утверждения либо отрицания (да и нет, true и false, 1 и 0). Переменная принадлежит множеству из 0 и 1 (xÎ{0;1}). Переменных может быть задано неограниченное количество (x1,x2,x3 и т.д.). При этом функция будет принимать значения только 0 и 1 (yÎ{0;1}). Функция может быть задана эвристически (словесно), при помощи таблицы истинности и аналитически.
Для одной переменной можно задать 4 функции, при этом таблица истинности будет иметь следующий вид:
| X | Y1 | Y2 | Y3 | Y4 |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Для n переменных можно задать 2n функций.
Функции Y1 и Y4 не представляют интереса, так как являются генераторами логических уровней, функция Y2 называется повторителем и записывается Y2=X, а функция Y3 – инвертором, и записывается 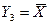 .
.
Для двух переменных соответственно можно записать шестнадцать функций.

| 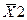
| X1 | X2 | Y1 | Y2 | Y7 | Y8 | Y15 | Y16 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
Нетрудно заметить, что таблица истинности симметрична относительно центра. То есть
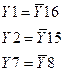
и т.д.
Рассмотрим функцию Y2, такая функция называется «И» - конъюнкция (объединение). Такая функция записывается Y2=X1×X2. Функция Y15 инверсна функции Y2,называется «И–НЕ» и записывается  .
.

Рисунок 1 – Элементы «И» и «И–НЕ»
Функция Y7 обозначается «ИЛИ» и называется функцией дизъюнкции (разъединения).
Функция дизъюнкции записывается Y7=X1+X2. Этой функции инверсна функция Y8, которая записывается 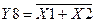 , и называется функцией «ИЛИ–НЕ».
, и называется функцией «ИЛИ–НЕ».
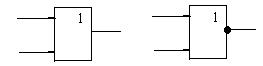
Рисунок 2 – Элементы «ИЛИ» и «ИЛИ–НЕ»
Закон де Моргана: Инверсия конъюнкций равна дизъюнкции инверсий. Четыре формы записи закона де Моргана:

Дата добавления: 2016-07-22; просмотров: 1964;











