РАСЧЕТ ТОЧНОСТИ РАЗМЕРНЫХ ЦЕПЕЙ.
При решении задач в области конструирования, изготовления, сборки, контроля и измерения параметров деталей и сборочных единиц выделяют две основные постановки задач размерных расчетов - прямую и обратную.
Прямая задача заключается в том, что при известных (заданных) параметрах замыкающего звена требуется определить значение параметров всех составляющих звеньев размерной цепи. Такая задача обычно появляется на этапе проектирования, при проектных расчетах.
При обратной задаче известны параметры всех составляющих звеньев размерной цепи и нужно определить параметры замыкающего звена. Обратные задачи возникают на этапе производства изделия и являются проверочными расчетами размерных цепей, т, е. решением обратной задачи проверяется правильность решения прямой задачи.
Конкретные выражения уравнений размерных цепей определяются видами размерных цепей, а также принятым методом расчета.
В настоящее время применяют два метода расчета (вычисления) параметров звеньев размерных цепей: метод максимума-минимума и вероятностный метод.
При расчете методом максимума-минимума учитывают только предельные размеры (отклонения) звеньев размерной цепи.
Недостатком метода максимума-минимума является очень малая вероятность совпадения действительных размеров параметр с их предельными размерами. Расчеты по этому методу приводят к повышенным требованиям к точности звеньев размерной цепи.
Вместе с тем метод достаточно прост и имеет широкое распространение в практике размерных расчетов.
При расчете вероятностным методом учитывают действительные или прогнозируемые законы рассеяния погрешностей звеньев размерных цепей и случайный характер их сочетания в размерных цепях. Вероятностный метод позволяет, задаваясь некоторой допустимой долей риска выхода замыкающего звена за установленные пределы, получить расширенные поля допусков составляющих звеньев размерной цепи по сравнению с методом максимума-минимума.
Расчет размерной цепи при обеспечении полной взаимозаменяемости методом максимума-минимума.
Проверочная задача
1. Определение номинального размера замыкающего звена.
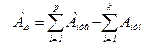
АD - замыкающее звено;
Аув - сборное звено, включающее все увеличивающие звенья;
Аум - сборное звено, включающее все уменьшающие звенья.
р,k - число соответственно всех увеличивающих и уменьшающих составляющих звеньев размерной цепи;
2. Определение допуска замыкающего звена.
TAD= AD max -AD min = ( Аув max - Аум min) – (Аув min - Аум max) =
= ( Аув max - Аум min) +(Аув min - Аум max) = T Аув + T Аум
3. Определение предельных отклонений замыкающего звена.
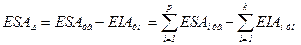
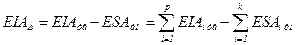
4. Определение предельных размеров замыкающего звена:
AD max= АD+ 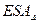 ; AD min= АD+
; AD min= АD+ 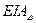
или 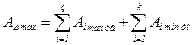 ;
; 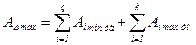
5. определение координат середины поля допуска:
 или
или 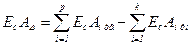
Дата добавления: 2020-10-14; просмотров: 635;











