РЕЗОНАНСНІ ЯВИЩА У ЛАНЦЮГАХ змінного СТРУМУ

Основні поняття й визначення

Під резонансом розуміють явища в ланцюгах перемінного струму, що містять елементи індуктивності і ємності, при якому реактивний опір або реактивна провідність дорівнюють нулеві. Резонанс, що виникає при послідовному з'єднанні елементів індуктивності і ємності, називають резонансом напруг, а при рівнобіжному з'єднанні – резонансом струмів. Ці явища в ланцюгах обумовлені взаємним перетворенням енергії електричного й магнітного полів.

Резонансні ланцюги широко застосовуються в електротехніці, вони є невід'ємною частиною ряду радіотехнічних пристроїв і часто використовуються в автоматиці й телемеханіці. Однак у ряді випадків явища резонансу небажані. Виникаючі, наприклад, в електричних ланцюгах і системах, вони можуть викликати перенапруги в окремих елементах, пробій ізоляцій та інші аномальні явища,

Резонанс напруг

Розглянемо явище резонансу в нерозгалуженому ланцюзі з опором, індуктивністю і ємністю (рис. 7.1, а). Умова резонансу в такому ланцюзі можна записати у виді:

,

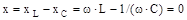(7.1)

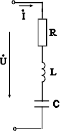
а) б)

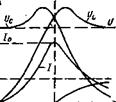
Рис. 7.1. Резонансний ланцюг (а) і її частотні характеристики (б)

Для режиму резонансу напруг характерно наступне:

Комплекс повного вхідного опору електричного ланцюга досягає мінімального значення, який дорівнює активному опору:

.

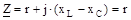Комплекс сили струму в ланцюзі досягає найбільшого значення і збігається по фазі з напругою:

.

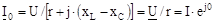Напруга на індуктивності дорівнює напрузі на ємності:

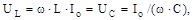
а через те, що їхні фази протилежні, вони в будь-який момент часу будуть компенсувати один одного; реактивні напруги на індуктивності й ємності при резонансі можуть перевищувати напругу мережі у стільки ж разів, у скільки кожний з реактивних опорів більше активного опору; напруга на активному опорі дорівнює напрузі на затисках ланцюга:

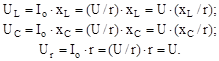
Кутова частота ω_о і частота f_o, при яких спостерігається явище резонансу, називаються власними резонансними частотами. Ці частоти, обумовлені з умови резонансу ω²·L·C=1, відповідно дорівнюють:

.

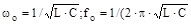(7.2)

(6.2)

Резонанс у ланцюзі може наступити тільки за рівності власної резонансної частоти ланцюга й частоти його джерела живлення.

З виразу для індуктивного і ємнісного опору при резонансі маємо:

.

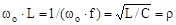(7.3)

Величина 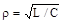, що має розмірність опору, називається хвильовим або характеристичним опором резонансного контуру. Хвильовий опір дорівнює й відношенню напруги U_L або U_C до сили струму I₀.

Відношення хвильового опору до активного опору називається добротністю Q контуру, а її зворотна величина — загасанням d:

.

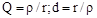(7.4)

Добротність дорівнює також відношенню U_L або U_C під час резонансу до повної напруги U.

Зміна величин, що характеризують роботу ланцюга, залежить від частоти джерела. Звичайно, залежності U_L, I, U_C і φ від кутової частоти ω при постійних U, r, L, C зображуються графічно.

Ці залежності, представлені на рис. 7.1, б, називаються резонансними кривими або частотними характеристиками резонансного контуру. Вони показують, що нерозгалужений ланцюг перемінного струму з L і С має вибірні властивості, тобто має найменший опір при частоті, близької до резонансної.

Резонанс струмів

Розглянемо найпростіший випадок паралельного з'єднання елементів із r,L і C (рис. 7.2, а). У такому ланцюзі резонанс струмів I настає за умови:

,

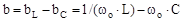(7.5)

де 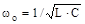— резонансна частота.

а) б)

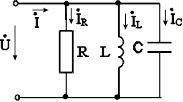
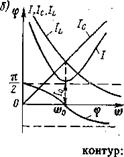
Рис. 7.2. Розгалужений резонансний контур:

a - схема; б - частотні характеристики

Для режиму резонансу струмів характерно наступне: комплекс повної вхідної провідності електричного ланцюга:

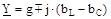
досягає мінімального значення, рівного активній провідності, тобто вхідний опір досягає максимуму; комплекс сили струму в нерозгалуженій частині електричного ланцюга:

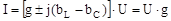
досягає мінімального значення і співпадає за фазою з напругою на вході ланцюга; сила струму у вітці з індуктивністю дорівнює силі струму у вітці з ємністю:

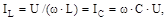
а через те, що їхні фази протилежні, вони в будь-який момент часу будуть компенсувати одна одну; реактивні сили струму віток:

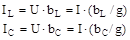
при резонансі можуть перевищувати силу струму в нерозгалуженій частині ланцюга у стільки разів, у скільки кожна з реактивних провідностей більше активної провідності; активна сила струму:

,

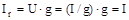тобто вона дорівнює силі струму в нерозгалуженій частині ланцюга.

З рівності індуктивної і ємнісної провідностей при резонансі маємо:

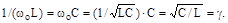
(7.6)

Величина 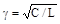, що має розмірність провідності, називається хвильовою провідністю резонансного контуру. Вона дорівнює також відношенню сили струму в галузі з індуктивністю або ємністю до напруги на вході ланцюга U.

Відношення хвильової провідності резонансного ланцюга до активної провідності називається добротністю Q, а її зворотна величина — загасанням d ланцюга, тобто:

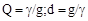
(7.7)

Добротність дорівнює також відношенню I_L або I_C при резонансі до сили струму I. Вона показує, у скільки разів сили струмів у реактивних галузях перевищують силу струму в нерозгалуженій частині в режимі резонансу.

Настроювання ланцюга у резонанс струмів, як і у резонанс напруг, можна здійснювати зміною індуктивності або ємності, або частоти. На рис. 7.2,6 зображені частотні характеристики розгалуженого резонансного контуру. У розгалуженому ланцюзі (рис. 7.3), що складається з двох паралельних віток, одна з яких складається з r і L, а інша з r і С, явище резонансу настає за умови b = b_L – b_C =0, що може бути записане так:

,

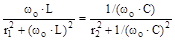(7.8)

звідси:

.

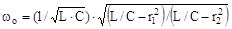(7.9)

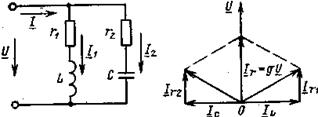
а) б)

Рис. 7.3. Змішаний резонансний ланцюг та його векторна діаграма

З цього виразу можна зробити наступні висновки: для одержання резонансу необхідно, щоб активні опори віток r₁ і r₂ були обидва більші або обидва менші хвильового опору 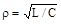. Якщо ця умова не дотримується, то не існує такої частоти, за якої резонанс мав би місце. При рівності активних опорів вітки і хвильового опору ( 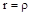) резонанс спостерігається при будь-якій частоті, тобто при всіх частотах струм у нерозгалуженій частині ланцюга збігається по фазі з напругою на затисках ланцюга і весь ланцюг виступає як активний опір; при незмінній частоті джерела живлення резонансу можна досягти зміною індуктивності, ємності й активного опору.