Змішане з'єднання приймачів

Будь-який приймач електроенергії практично може мати два або три параметри одночасно. На рис. 5.6, а представлений ланцюг із двох паралельних віток, одна з яких містить активний опір і індуктивність, а інша – активний опір і ємність. Якщо в такий ланцюг подати синусоїдальну напругу u = U_m·sinωt, то сили струмів у паралельних вітках будуть відповідно дорівнювати:

i₁ = I_1m ·sin (ωt –φ₁); i₂ = I_2m ·sin (ωt - φ₂ ).

Діючі значення сил струмів визначаються за законом Ома. Складова і повна сила струму нерозгалуженої частини ланцюга відповідно запишуться у такий спосіб:

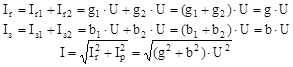
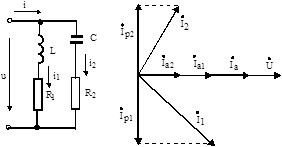
а) б)

Рис. 5.6. Розгалужений ланцюг і його векторна діаграма

Лекція 6

Символічний метод розрахунку електричних

Ланцюгів

Символічний метод розрахунку ланцюгів перемінного струму, в основу якої покладено зображення синусоїдальних функцій часу комплексними числами, дозволяє рівняння для будь-якого ланцюга, складені на підставі законів Кірхгофа, вирішувати алгебраїчно, аналогічно рівнянням для ланцюгів постійного струму. Це значно спрощує розрахунки ланцюгів перемінного струму, особливо складних ланцюгів.

Відомо, що комплексне число може бути записане в трьох основних формах — алгебраїчній, тригонометричній і показовій:

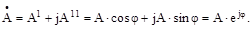
(6.1)

Комплекси, що зображують синусоїдальні величини, прийнято позначати відповідними прописними буквами з рискою внизу або крапкою вгорі, наприклад 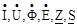. Таким чином, якщо сила струму і напруга синусоїдальні, тобто 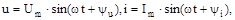то відповідні їм комплекси амплітуд і діючих значень запишуться так:

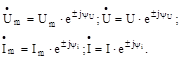
(6.2)

Відношення комплексу напруги до комплексу сили струму називається комплексом повного опору, тобто:

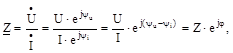
(6.3)

де Z- повний опір, чи модуль комплексу повного опору;

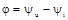– кут зрушення між векторами напруги і сили струму.

Отже, комплекс повного опору може бутипредставлений виразом:

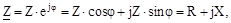
де R и X–відповідно активний і реактивний опори.

Відношення комплексу сили струму до комплексу напруги називається комплексом повної провідності, тобто:

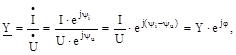
де Y — повна провідність ланцюга, чи модуль комплексу повної провідності.

Отже, комплекс повної провідності ланцюги може бути виражений співвідношенням:

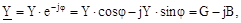
(6.4)

де Gі B — відповідно активна і реактивна провідності ланцюга.

У символічній формі можуть бути представлені також повна, активна і реактивна потужності. Для цього при відомих комплексах напруги й сили струму 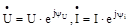треба помножити комплекс напруги на сполучений комплекс сили струму :

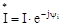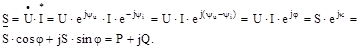
(6.5)

Отже, модуль комплексу S визначає повну потужність, дійсна частина – активну, а уявна – реактивну.

Закон Ома для ланцюгів перемінного струму в символічній формі може бути представлений у наступному виді:

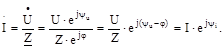
(6.6)

Ці співвідношення справедливі для всякого лінійного ланцюга і для будь-якої його ділянки.

Перший закон Кірхгофа в символічній формі запису говорить: алгебраїчна сума комплексів сил струмів, що сходяться у вузлі електричного ланцюга, дорівнює нулю:

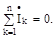
(6.7)

Другий закон Кірхгофа в символічній формі для будь-якого замкнутого контуру записується у виді рівняння:

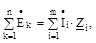
(6.8)

таким чином, алгебраїчна сума комплексів ЕРС, що діють у контурі, дорівнює алгебраїчній сумі комплексів падінь напруг на всіх ділянках цього контуру..

При складанні рівнянь за законами Кірхгофа правила знаків для комплексів сил струмів, ЕРС і напруг ті ж, що і для векторів.

Розглянемо теоретичний розрахунок деяких ланцюгів перемінного струму. Нехай електричний ланцюг, зображений на рис. 6.1, а, знаходиться під синусоїдальною напругою 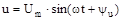. Визначимо силу струму в ланцюзі, а також побудуємо векторні діаграми для індуктивного (φ>0) і ємнісного (φ<0) характеру опору, представлені відповідно на мал. 6.1, б, в.

На підставі другого закону Кирхгофа рівняння електричної рівноваги ланцюга для комплексних величин запишеться так:

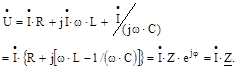
(6.9)

Вирішуючи це рівняння щодо комплексу діючого значення сили струму, одержимо:

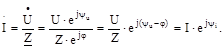
(6.10)

де 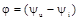– початкова фаза сили струму.

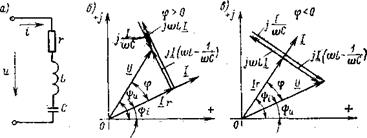
а) б) в)

Рис. 6.1. Нерозгалужений ланцюг з елементами R, L и С та його

векторні діаграми

Аргумент ф і модуль Z, комплексу повного опору знаходяться з виразів:

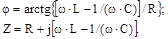
(6.11)

Комплекс потужності визначається формулою:

(6.12)

На мал. 6.1, б, в для розглянутого ланцюга побудовані векторні діаграми.

Якщо нерозгалужений ланцюг складається з n послідовно з'єднаних ділянок, комплекси повних опорів яких Z, Z₂, Zз і знаходиться під синусоїдальною напругою 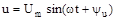, то по другому закону Кірхгофа можна записати:

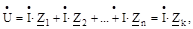
(6.13)

де 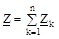, тобто комплекс повного опору нерозгалуженого ланцюга дорівнює алгебраїчній сумі комплексів повних опорів ділянок ланцюга.

З рівняння (6.13) знаходимо комплекс сили струму:

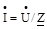
Комплекс потужності розглянутого електричного ланцюга можна знайти, множачи комплекс напруги 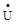на сполучений комплекс сили струму :

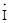Якщо ланцюг складається з п рівнобіжних (паралельних) віток, комплекси повних провідностей яких Y, Y, . -., Y_n(мал. 6.2), то, на підставі першого закону Кірхгофа, комплекс сили струму у нерозгалуженій частині ланцюга визначиться виразом:

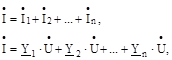
де 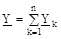, тобто комплекс еквівалентної провідності розгалуженого ланцюга дорівнює алгебраїчній сумі комплексів повних провідностей віток.

Наслідком першого закону Кірхгофа є співвідношення:

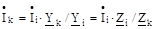
тобто сила струму у вітках прямо пропорційна їхнім комплексам повних провідностей і обернено пропорційна комплексам повних опорів.

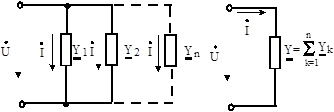
Рис. 6.2 Паралельне з'єднання елементів

Комплекс потужності розгалуженого електричного ланцюга визначається виразом:

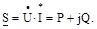
ЛЕКЦІЯ 7