Основні закони електричних ланцюгів

Основними законами ланцюгів постійного струму є закон Ома і два закони Кірхгофа.

Закон Ома.Закон Ома для замкнутого ланцюга, що складається з послідовно з'єднаних п опорів і джерела напруги (рис. 2.1), має вигляд:

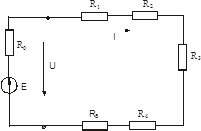
Рис. 2.1. До визначення закону Ома

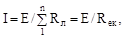
(2.1)

де R_ек — еквівалентний опір ланцюга. Отже, струм прямо пропорційний ЕРС і назад пропорційний сумі опорів усього ланцюга.

Для ділянки ланцюга закон Ома записується в такий спосіб:

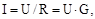
(2.2)

тобто струм прямо пропорційний напрузі на затисках ділянки й обернено пропорційний його опорові.

З формули закону Ома випливає важливе співвідношення: напруга на затисках джерела дорівнює різниці між ЕРС і спаданням напруги усередині джерела, тобто:

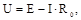
(2.3)

де R_о — внутрішній опір джерела.

Закони Кірхгофа. Перший закон Кірхгофа встановлює залежність між силами струмів, що сходяться у вузлах розгалуженого електричного ланцюга, і для n галузей у вузлі записується у виді рівняння:

,

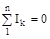(2.4)

тобто алгебраїчна сума сил струмів, що сходяться в будь-якому вузлі електричного ланцюга, дорівнює нулеві.

При підсумовуванні сил струмів необхідно враховувати їхні напрямки: усі струми, що течуть до вузла, беруться з однаковим знаком, наприклад позитивним, і всі струми, що течуть від вузла, – з негативним. Для вузла схеми, поданої на рис. 2.2, а, рівняння (2.4) приймає вид:

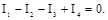
Другий закон Кірхгофа встановлює залежність між ЕРС, що діють у замкнутому контурі, і спаданнями напруги на елементах цього контуру. Математично ця залежність для контуру, що має т джерел ЕРС і n пасивних елементів, записується формулою:

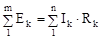
(2.5)

тобто алгебраїчна сума ЕРС, що діють у будь-якому замкнутому контурі, дорівнює алгебраїчній сумі падінь напруги на всіх ділянках цього контуру.

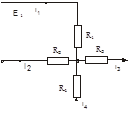
а) б)

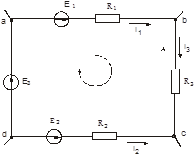
Рис. 2.2. До визначення першого (а) і другого (б)законів Кірхгофа

Для визначення знаків додатків необхідно обійти замкнутий контур у будь якому напрямку. Сили струмів й ЕРС, що збігаються з напрямком обходу, узяти з одним знаком (наприклад, "+ "), а струми й ЕРС, що мають напрямок, протилежний напрямкові обходу, узяти з протилежним знаком (" - "). Наприклад, для контуру abcd складного ланцюга (рис. 3.2, б), роблячи обхід у напрямку стрілки, показаної усередині контуру,

одержимо рівність: