Метод вузлових потенціалів

Метод зводиться до визначення потенціалів окремих вузлів складного електричного ланцюга шляхом розв’язання системи рівнянь, складених за першим законом Кірхгофа. Застосування цього методу дозволяє зменшити кількість рівнянь до числа "Y", що дорівнює кількості вузлів без одного: Y= N – 1.

При написанні рівнянь один із вузлів приймають за опорний і потенціал його вважають рівним нулеві, а потенціали інших вузлів (вузлових потенціалів) визначають шляхом розв’язання системи рівнянь. Після знаходження вузлових потенціалів сили струмів у вітках визначають за законом Ома або виходячи з другого закону Кірхгофа. Розглянемо застосування методу до розрахунку складних ланцюгів.

Нехай будь-який лінійний ланцюг (рис. 3.3) має три вузли і п'ять віток. Виберемо довільно опорний вузол і позначимо його через 0, а інші вузли – цифрами 1 і 2. Потенціал точки 0, φ₀ = 0 В.

Система рівнянь у загальному виді буде такою:

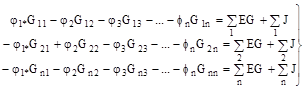
(3.2)

Тут 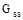– сума провідностей віток, підключених до вузла s, а G_qs – сума провідностей віток, ізо з'єднують вузол s з вузлом q;

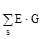– алгебраїчна сума здобутків віток, приєднаних до вузла s, причому "+", якщо ЕРС спрямована до вузла s, "-" – якщо від вузла;

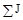- алгебраїчна сума джерел струму, приєднаних до вузла s, причому "+", якщо J спрямована до вузла s, "-" – якщо від вузла.

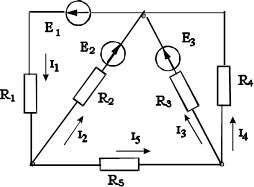
Рис. 3.3. Схема ланцюга до розрахунку методом вузлових

потенціалів

У випадку двох вузлів А і В у ланцюзі вузлова напруга U_ав визначиться за виразом:

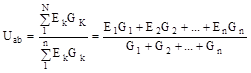
(3.3)

У рівнянні 3.3 добутки Е_kG_k беруться зі знаком "+", якщо ЕРС направлені від вузла А до вузла В.

Струми розраховуються за законом Ома або виходячи з другого закону Кірхгофа.