Метод контурних струмів
Метод зводиться до розв’язання системи n = p – q + 1 рівнянь, складених за другим законом Кірхгофа для незалежних контурів ланцюга. У результаті рішення визначаються сили струмів, що протікають по незалежних контурах, звані контурними силами струмів. Дійсні ж сили струмів у вітках знаходяться як алгебраїчна сума відповідних контурних сил струмів. На рис. 3.2 зображено складний ланцюг, що має шість віток і чотири вузли. Для визначення сил струмів у вітках ланцюга визначаємо число незалежних контурів n=p-q+1=6-4+1=3. Вибравши контури та задавши у них напрямки контурних струмів J1, J2, J3, як зазначено на рисунку стрілками, складемо рівняння за другим законом Кірхгофа:
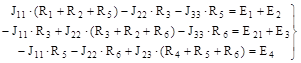
| (3.1) |
У цих рівняннях прийнято називати й позначати:
а) суму всіх опорів кожного контуру – власним опором контуру:
R11 = R1 + R3 + R5; R22 = R2 + R3 + R6; R33 = R4 + R5 + R6;
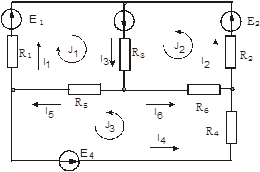
Рис. 3.2. Схема ланцюга до розрахунку методом контурних
струмів
б) опір спільної вітки двох контурів — взаємним опором контурів; він вважається позитивним, якщо контурні струми в ньому збігаються по напрямку, і негативним, якщо контурні струми в цьому опорі протилежні за напрямком:
R12 = R21 = R3; R13 = R31 = R5; R23 = R32 = R6;
в) алгебраїчну суму ЕРС у контурі — контурною ЕРС:
E11 = E1 + E3; E22 = E2 + E3; E33 = E4.
З урахуванням уведених позначень рівняння (3.1) перепишуться у такий спосіб:
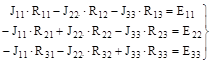
Дата добавления: 2020-10-14; просмотров: 701;











