ЭЛЕМЕНТЫ И ПАРАМЕТРЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА
1. ЦЕПЬ С АКТИВНЫМ СОПРОТИВЛЕНИЕМ
На рис. 67 в цепь переменного тока включен элемент, обладающий только активным сопротивлением r (лампа накаливания, угольный резистор, электронагревательный прибор и т.д.). Пусть подаваемое в схему напряжение синусоидально и изменяется по закону u =Um sinwt. Схема идеализированная, следовательно, L = C = 0.

Рис. 67 Однофазная электрическая цепь с активным сопротивлением: а – схема, б, в - временная и векторная диаграммы.
Ток в цепи. Согласно закона Ома, в цепи протекает переменный ток, мгновенное значение которого определяется выражением:
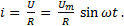 (6-1)
(6-1)
Обозначим 
Тогда  (6-2)
(6-2)
где 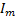 – амплитудное значение тока,
– амплитудное значение тока,  –циклическая частота.
–циклическая частота.
Из выражений для напряжения и тока видно, что эти величины синфазны и разность фаз между ними φ=0. Совпадение фаз тока и напряжения в цепи с активной нагрузкой означает совпадение во времени нулевых и амплитудных значений.
Закон Ома в комплексном виде. Комплексы действующих значений тока и напряжения
İ =I  и Ù = U
и Ù = U  , соответственно.
, соответственно.
Комплекс сопротивления Ż = Ù/İ = U/I 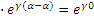 =
=  - γ
- γ 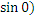 = U/I = R. (6-3)
= U/I = R. (6-3)
Комплексное сопротивление резистивного элемента является положительным действительным числом, численно равным активному сопротивлению.
Уравнение мощности. Произведение мгновенного значения напряжения на мгновенное значение тока в любой момент времени равно мгновенному значению мощности:
р = u i. (6-4)
Так как u =Um sinwt; i =Im sinwt, то
р = Im sinwt Um sinwt = Im Um sin2wt. (6-5)
Понизим степень функции синуса, получим sin2wt = (1 - 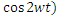 /2.
/2.
P =UmIm (1 - 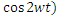 /2 =UI (1 -
/2 =UI (1 - 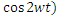 = UI – UI
= UI – UI  . (6-6)
. (6-6)
Данное выражение показывает, что кривая мгновенной мощности колеблется с удвоенной частотой 2ω по сравнению с кривыми тока и напряжения.
 Рис. 68
Рис. 68
Из рис. видно, что за один период изменения тока, мощность изменяется дважды, оставаясь положительной (график мощности выше оси абсцисс) как при i >0, так и при i <0. Максимальных значений мощность достигает в те моменты времени, когда максимальны напряжения и ток, а нулевое, когда напряжение и ток равны нулю.
Положительные значения мощности свидетельствуют о том, что электрическая энергия забирается от источника энергии и преобразуется в тепловую. Причем скорость потребления энергии с течением времени не остается постоянной, а изменяется по закону р = UI (1 - 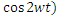 .
.
Средняя мощность. Средняя мощность за период времени
Рср = Р = 1/T∙  = 1/T∙UI
= 1/T∙UI 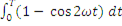 . (6-7)
. (6-7)
Так как интеграл  то
то
P = 1/T∙ 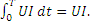 (6-8)
(6-8)
Cредняя мощность, выделяемая за время равное периоду в цепи с чисто активной нагрузкой называется активной мощностью, которая измеряется в ваттах (ВТ). Последнюю формулу можно представить и в таком виде:
P = UI = I2R = U2/R. (6-9)
2. ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ С ИНДУКТИВНОСТЬЮ
Рассмотрим идеальную катушку индуктивности, для которой Rk =C = 0 (Rk – активное сопротивление катушки, С – межвитковая емкость). L – индуктивность катушки. Пусть напряжение u = Um 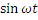 . По цепи протекает переменный ток. Так как ток в цепи изменяется, следовательно в катушке индуцируется эдс индукции eL = -L di/dt. Уравнение электрического
. По цепи протекает переменный ток. Так как ток в цепи изменяется, следовательно в катушке индуцируется эдс индукции eL = -L di/dt. Уравнение электрического
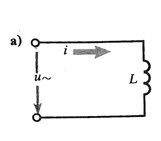
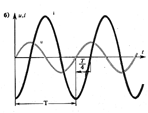

Рис. 69 Цепь переменного тока с индуктивным элементом: а – схема, б.в – временная и векторная диаграммы.
состояния имеет вид
u + eL = I Rk = 0. (6-10)
Откуда следует, что u = - eL = L di/dt.
Из уравнения следует, что для любого момента времени (u) численно равна (eL) и эти величины находятся в противофазе.
di = u/L dt = Um  . (6-11)
. (6-11)
Проинтегрируем последнее выражение 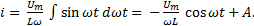
А – постоянная интегрирования, которая при отсутствии постоянной составляющей тока равна нулю.
Заменим -  =
=  .
.
Тогда мгновенное значение тока приобретает вид:
i = Um/ωL sin(𝜔𝑡− 𝜋/2).
Обозначим Um/ωL = Im.
В окончательном виде выражение для тока в цепи с индуктивным элементом
i = Im  . (6-12)
. (6-12)
Из сравнения аналитических уравнений напряжения и тока следует, что в результате возникновения в цепи эдс индукции между этими характеристиками возникает фазовый сдвиг равный π/2 или напряжение опережает ток на угол π/2. Это означает, что с нарастанием напряжения от нуля до максимума ток падает по абсолютной величине от максимума до нуля и наоборот (рис. б).
На векторной диаграмме (рис. в), если вектор тока располагается горизонтально, то вектор напряжения – с опережением по фазе на угол π/2.
Индуктивное сопротивление. Произведение  - называется индуктивным сопротивлением, которое пропорционально частоте тока (ω =2πν) и индуктивности элемента цепи.
- называется индуктивным сопротивлением, которое пропорционально частоте тока (ω =2πν) и индуктивности элемента цепи.
Измеряется индуктивное сопротивление в омах (Ом).
Таким образом, любой элемент цепи, обладающий индуктивностью, создает определенное сопротивление при прохождении через него переменного тока. Это можно пояснить тем, что в индуктивном элементе при прохождении переменного тока происходит возбуждение эдс индукции eL, которая согласно правила Ленца своим действием направлена против причины, ее порождающей, следовательно, она создает препятствие на пути движения тока. Хотя индуктивное и активное сопротивления имеют одинаковые размерности, причины, их порождающие, различны.
Индуктивное сопротивление – это сопротивление, которое оказывает току индуктированная эдс, возникающая в этом элементе при прохождении через него переменного тока.
Для постоянного тока ν=0 и, следовательно,  =0. Для переменного тока, с изменяющейся
=0. Для переменного тока, с изменяющейся

Рис. 70 Частотная зависимость индуктивного сопротивления.
частотой от нуля до бесконечности величина  увеличивается по линейному закону от
увеличивается по линейному закону от  = 0 до
= 0 до  = ∞ (рис. )
= ∞ (рис. )
Уравнение мощности. В цепи с индуктивным элементом мгновенное значение мощности
p = ui = Im ,sin-(𝜔𝑡− 𝜋/2). Um 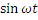 = - Im
= - Im  Um ,sin-𝜔𝑡. (6-13)
Um ,sin-𝜔𝑡. (6-13)
Заменим 
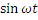 =
= 
Получим p = - UmIm/2 ∙  = - UI
= - UI 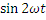 . (6-14)
. (6-14)
Это выражение показывает, что кривая мощности изменяется по закону синуса, но с двойной частотой 2ω.
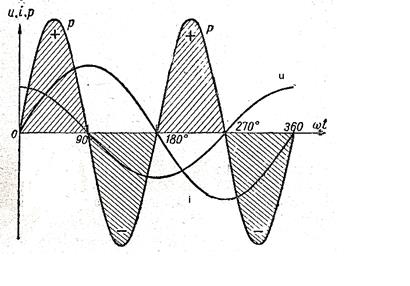
Рис. 71 Кривые мгновенных значений напряжения, тока и мощности для цепи, содержащей индуктивность.
Когда u и i имеют одинаковые знаки (рис.71 ), то кривая р положительна и располагается выше оси абсцисс. Если же u и i имеют разные знаки, то кривая р отрицательна и располагается ниже оси абсцисс.
В первую четверть периода ток, а вместе с ним и магнитный поток катушки увеличивается. Катушка забирает от источника энергии мощность. В это время энергия забираемая от источника идет на создание магнитного поля (мощность положительна). Количество энергии, запасаемое в магнитном поле за время роста тока, можно определить как :
 (6-15)
(6-15)
За вторую четверть периода ток убывает. ЭДС индукции, которая в первую четверть периода стремилась помешать возрастанию тока, теперь, когда ток начинает убывать, будет мешать ему уменьшаться. Сама катушка становится как бы генератором электрической энергии. Она возвращает источнику энергию, запасенную в ее магнитном поле. Мощность отрицательна и кривая р располагается ниже оси абсцисс.
За вторую половину периода явление повторяется. Таким образом, между источником переменного напряжения и катушкой, содержащей индуктивность, происходит обмен мощностью. В течение первой и третьей четвертей периода мощность поглощается катушкой, в течение второй и четвертой четвертей мощность, в равной степени, возвращается источнику.
В этом случае, в среднем, расхода мощности не будет, несмотря на то, что на зажимах цепи есть напряжение U и в цепи протекает ток I.
Вычислим активную мощность за время равное периоду
P = 1/T 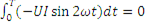
(интеграл от синусоидальной функции в пределах двух периодов равен нулю).
Тот же результат мы получим, если вычислим активную мощность по формуле
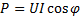 . (6-16)
. (6-16)
Так как между напряжением и током существует фазовый сдвиг равный 900 и 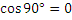 .
.
Поэтому активная мощность также равна нулю, т.е. расхода мощности нет.
Реактивная (индуктивная) мощность количественно оценивается амплитудой кривой мощности:
QL = U I  = I2 XL. (6-17)
= I2 XL. (6-17)
и измеряется - вольт-ампер реактивный (вар).
4. ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ С ЕМКОСТНЫМ ЭЛЕМЕНТОМ.
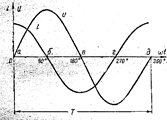
На рис. 72 в цепь переменного тока включен идеальный элемент, обладающий только емкостью С. Активным и индуктивным сопротивлениями этого элемента пренебрегаем, т.е. Rc = L = 0.

а б в
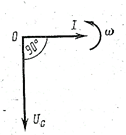
Рис. 72 Цепь переменного тока с емкостным элементом: а- схема, б,в – временная и векторная диаграммы.
При подключении пременного напряжения u = Um  вследствие периодической перезарядки конденсатора в цепи проходит ток, который можно определить как скорость изменения заряда на обкладках конденсатора.
вследствие периодической перезарядки конденсатора в цепи проходит ток, который можно определить как скорость изменения заряда на обкладках конденсатора.
Уравнение тока.
i =dq/dt, (6-18)
т.к емкость конденсатора C=q/uc, то dq = C duc.
Тогда i =dq/dt = C∙duc/dt. В цепи для любого момента времени выполняется соотношение u=uc = Um  . С учетом этого
. С учетом этого
i =C d(Um  )/dt. (6-19)
)/dt. (6-19)
Продифференцировав это выражение, получим
i =CUmω  .
.
Обозначим  = Im
= Im
и выражение для тока примет вид:
i = Im  . (6-20)
. (6-20)
Таким образом, в цепи с емкостным элементом кривая тока опережает кривую напряжения по фазе на угол π/2. Это означает, что с нарастанием напряжения от нуля до максимума ток падает от максимума до нуля (рис.72 б).
Действующее значение тока определим из соотношения:
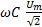

или
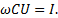 (6-21)
(6-21)
Напряжение и ток в рассматриваемой цепи можно изобразить с помощью векторной диаграммы (рис. в). Если вектор тока расположить горизонтально (удобно для сравнения с предыдущими векторными диаграммами), то вектор напряжения, отстающий по фазе на угол  откладывается вниз.
откладывается вниз.
Емкостное сопротивление. Изуравнения ( 6-21) следует
U/I = 1/ωC, (6-22)
где 1/ωC = Xc – емкостное сопротивление.
Следовательно,
Xc = 1/ωC = 1/2πνC. (6-23)
Емкостное сопротивление обратно пропорционально частоте и емкости элемента, т.е. с увеличением частоты от нуля до бесконечности величина Xc уменьшается от бесконечности до нуля.
Измеряется это сопротивление в омах (ом)
Емкостное сопротивление – это сопротивление току, которое оказывает электрическое поле, возникающее вокруг накапливаемого на пластинах конденсатора заряда.
Закон Ома в комплексном виде. Комплекс напряжения Ù = U  . Комплекс тока Í = I
. Комплекс тока Í = I  . Комплекс сопротивления Ż = Ù/Í = U/I ∙
. Комплекс сопротивления Ż = Ù/Í = U/I ∙ 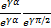 = Xc
= Xc  = (
= ( 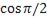 -
-  ) = -
) = -  .
.
Ù = -  Í. (6-24)
Í. (6-24)
Комплекс сопротивления электрической цепи с конденсатором является отрицательным мнимым числом, модуль которого равен  .
.
Уравнение мощности. Если в цепь переменного тока включен только конденсатор, то уравнения для мгновенных значение напряжения и тока запишутся как
u = Um 
и
i = Im  .
.

Рис. 73
Тогда
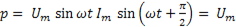
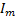


Подставляя в это выражение 
 =
= 
 получим
получим
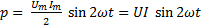 . (6-25)
. (6-25)
Мощность в рассматриваемой цепи изменяется аналогично мощности в цепи с индуктивным элементом, т.е. синусоидально с удвоенной частотой 2ω. Как следует из рис. 73 , мощность положительна (вторая и четвертая четверти периода), когда ток и напряжение имеют одинаковые знаки, и отрицательна (первая и третья четверти периода, когда ток и напряжение имеют различные знаки. Кроме того, во время увеличения абсолютного значения напряжения мощность цепи положительна, а во время его уменьшения – отрицательна. Это объясняется тем, что с увеличением напряжения конденсатор заряжается, между его пластинами создается электрическое поле и увеличивается энергия, запасенная этим полем (ток уменьшается). 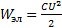 . Когда конденсатор разряжается, энергия поля уменьшается, переходит в электрическую и возвращается к источнику питания (ток возрастает).
. Когда конденсатор разряжается, энергия поля уменьшается, переходит в электрическую и возвращается к источнику питания (ток возрастает).
Мощность, как скорость преобразования энергии отображает процесс преобразования электрической энергии источника и энергии электрического поля конденсатора.
Таким образом, в цепи с емкостным элементом происходит периодический обмен энергии без преобразования электрической энергии источника в тепловую или механическую.
Активная мощность рассматриваемой цепи:
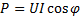 =0.
=0.
Так как в цепи с конденсатором ток опережает напряжение на 900, то φ = 900;  Поэтому активная мощность также равна нулю, т.е. в такой цепи , как и в цепи с чистой индуктивностью, расхода мощности нет.
Поэтому активная мощность также равна нулю, т.е. в такой цепи , как и в цепи с чистой индуктивностью, расхода мощности нет.
Для установления скорости обмена энергии в рассматриваемой цепи аналогично цепи с индуктивным элементом вводится понятие реактивной (емкостной) мощности:
 = UI
= UI 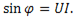 (6-26)
(6-26)
Реактивная мощность измеряется в варах.
5. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ R, L, C – ЭЛЕМЕНТОВ.
На рис.74 в цепь переменного тока последовательно включены резистор, идеальная катушка индуктивности и идеальный конденсатор. Эту цепь можно представить как последовательное соединение активного сопротивления R , индуктивного сопротивления XL и емкостного сопротивления Xc.

Рис.74
Уравнение напряжений. При протекании в цепи синусоидального тока
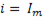
 (6-27)
(6-27)
на каждом элементе цепи создается падение напряжения: на резисторе – активное падение напряжения Ua = UR; на катушке – индуктивное падение напряжения UL; на конденсаторе - емкостное падение напряжения Uc.
Мгновенное значение полного (общего или результирующего) значения напряжения в любой момент времени
u = ua + uL + uc . (6-28)
Причем активная составляющая напряжения
 (6-29)
(6-29)
индуктивная
 =
=  (6-30)
(6-30)
емкостная
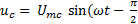 ). (6-31)
). (6-31)
Результирующее напряжение
 +
+ 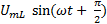 +
+  ). (6-31)
). (6-31)
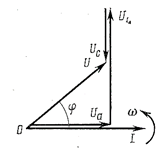
Для нахождения амплитудного или действующего значения результирующего напряжения и фазового сдвига между напряжением и током воспользуемся векторной диаграммой действующих значений напряжений. Построение осуществляется в такой последовательности:
1) вектор тока Iоткладывается по горизонтальной прямой, так как его начальная фаза равна нулю;
2) вектор Ua совпадает по фазе с вектором I;
3) от конца вектора Uaоткладывается вектор UL, направленный вертикально вверх (начальная фаза +π/2);
4) от конца вектора UL откладывается вектор Uc, направленный вертикально вниз (начальная фаза –π/2);
5) складывая векторы Ua, UL, Uc, получаем вектор результирующего напряжения цепи
U = Ua + UL + Uc. (6-32)
Модуль результирующего напряжения находится из прямоугольного треугольника:
 . (6-33)
. (6-33)
Нахождение результирующего напряжения с использованием векторного сложения напряжений на отдельных участках цепи возможно с использованием правила параллелограмма.
а б
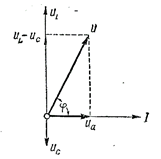
Рис. 75 Диаграммы напряжений для R, L, C – цепи.
Напряжения  и
и  сдвинуты по фазе на 1800 (находятся в противофазе). Поэтому при геометрическом сложении векторов они взаимно вычитаются. Векторная разность
сдвинуты по фазе на 1800 (находятся в противофазе). Поэтому при геометрическом сложении векторов они взаимно вычитаются. Векторная разность 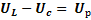 называется реактивным напряжением. Складывая вектора
называется реактивным напряжением. Складывая вектора 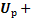 Uaпо правилу параллелограмма, находим величину и направление вектора результирующего напряжения U.
Uaпо правилу параллелограмма, находим величину и направление вектора результирующего напряжения U.
Анализируя векторную диаграмму напряжений для RLC-цепи, можно сделать вывод, что при UL > Uc вектор результирующего напряжения опережает вектор тока на угол φ < 900, а при UL < Uc результирующий вектор напряжения отстает от вектора тока на угол φ < 900.
Из треугольника напряжений тригонометрические функции угла сдвига фаз можно записать в виде:
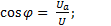

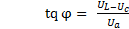 ; (6-34)
; (6-34)
Треугольник сопротивлений. Поделив каждую сторону треугольника напряжений на одно и то же число (на ток) получим подобный треугольник – треугольник сопротивлений для RLC-цепи, т.е.  ; полное сопротивление
; полное сопротивление 
Величина полного напряжения определяется выражением 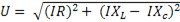 , а ток в цепи равен
, а ток в цепи равен
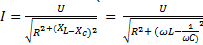 . (6-35)
. (6-35)
Тогда полное сопротивление последовательной RLC-цепи равно:
 . (6-36)
. (6-36)
Из треугольника сопротивлений следует, что фазовый сдвиг между током и полным напряжением определяется из условия:
 . (6-37)
. (6-37)
Видно, чем больше активное сопротивление, тем меньше сдвиг фаз.
Уравнение мощности. Треугольник мощностей. Для построения треугольника мощностей умножим все стороны треугольника напряжений на ток 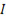 . Тогда активная мощность
. Тогда активная мощность
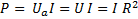 . (6-38)
. (6-38)
Измеряется активная мощность в ваттах (ВТ).
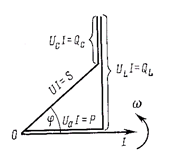
Рис.76
Индуктивная мощность
 =
= 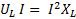 . (6-39)
. (6-39)
Емкостная мощность
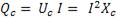 . (6-40)
. (6-40)
Полная реактивная мощность
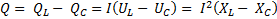 . (6-41)
. (6-41)
Измеряется реактивная мощность – вольт –ампер - реактивный (ВАР)
Полная мощность цепи
 (6-42)
(6-42)
Измеряется полная мощность - вольт на ампер (ВА).
Дата добавления: 2020-10-14; просмотров: 875;











