СЛОЖЕНИЕ СИНУСОИДАЛЬНЫХ ВЕЛИЧИН

На практике часто приходится складывать синусоидальные токи, напряжения, эдс и другие величины.

Определим переменный ток iкак сумму нескольких переменных токов и сначала аналитически, а затем используя векторный метод.

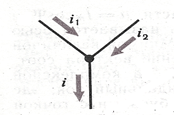
Рис.64 Схема узла электрической цепи

Аналитический метод. Для аналитического сложения необходимо произвести алгебраическое сложение их мгновенных значений. Из закона Кирхгофа следует, что общий ток

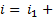
(5-3)

Пусть и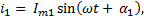

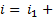
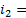
Упростим задачу и положим, что

Тогда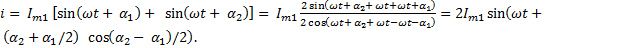

Обозначим .

Тогда в окончательном виде :

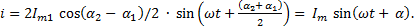(5-4)

Откуда видно, что в результате сложения двух синусоидальных токов результирующий (общий) ток имеет ту же частоту ω, амплитуду равную I_m и начальную фазу α.

Векторный метод. Для сложения двух синусоидальных величин, заданных векторами, необходимо произвести геометрическое суммирование этих векторов, пользуясь правилом параллелограмма, т.е.

Рис. 65

Из рис. 65 следует, что при сложении двух векторов, вращающихся с одинаковой частотой ω, результирующий вектор вращается с той же частотой.

Для определения результирующей амплитуды при векторном сложении двух синусоидальных величин, сдвинутых по фазе, необходимо воспользоваться теоремой косинусов.

Тогда

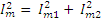
( 5-5)

где α₂ – α₁ = φ –сдвиг фаз между синусоидальными величинами.

Начальную фазу результирующего вектора α определим из соотношения

. (5-6)

Для случая из уравнения (5-5) следует:

Откуда

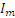
Далее определим начальную фазу результирующего вектора

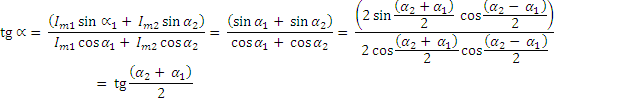
или

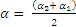. (5-7)

Таким образом, используя графический метод мы получили тот же самый результат, что и в случае решения задачи аналитическим методом (см. ур. 5-4 ).

Метод комплексных чисел. Комплексы амплитуды первого и второго токов в тригонометрической форме

Í_m1 = I_m1 (cosα₁ + γsinα₁) и Í_m2 = I_m2 (cosα₂ + γsinα₂). (5-8)

Комплекс результирующего тока

Í_m = Í_m1 + Í_m2 = I_m1[(cosα₁ + cosα₂) + γ (sinα₁ + sinα₂)] . (5-9)

Сумма косинусов cosα₁ + cosα₂ = 2 cos(α₂ +α₁)/2 ∙ cos(α₂ – α₁)/2.

Сумма синусов sinα₁ + sinα₂ = 2 sin (α₂ +α₁)/2∙cos (α₂ –α₁)/2.

Тогда Í_m =2I_m1∙ cos (α₂ –α₁)/2 [cos(α₂ +α₁)/2 +γ sin (α₂ +α₁)/2.

Обозначим 2I_m1∙ cos (α₂ –α₁)/2 =Im и α = (α₂ + α₁)/2.

Получим Í_m = I_m (cosα + γsinα) = I_me^γα.

Откуда мгновенное значение результирующего тока

i = i₁ + i₂ = I_m sin(ωt + α). (5-10)