Условия резонанса напряжений
1. Необходимо последовательное соединение катушки индуктивности, обеспечивающей R и XL, и конденсатора, обеспечивающего ХС. Это так называемый последовательный контур.
2. Необходим источник синусоидального тока с частотой wС.
3. Необходимо, чтобы частота источника совпадала с собственной частотой контура (резонансной частотой — w0). Резонансную частоту можно определить из условия ХL = XC, т. е. Lw0 =  , откуда w0=
, откуда w0=  .
.
wС = w0 — необходимое условие резонанса, но не достаточное.
Признаки резонанса
1. Ток и напряжение, приложенное к цепи, совпадают по фазе j = 0.
2. Сопротивление контура минимальное и чисто активное Z = R.
3. Ток в цепи максимален, т. к. 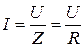 → Imax
→ Imax
4. Падение напряжения на активном сопротивлении равно приложенному к контуру напряжению, а именно: UR= IR = IZ = U.
5. Падения напряжений на индуктивности и ёмкости равны по амплитуде, противоположны по фазе и больше (или значительно больше) приложенного напряжения:
UL = IXL = IXC >> U = IR.
При этом коэффициент усиления по напряжению:
 ,
,
где 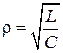 — характеристическое волновое сопротивление контура;
— характеристическое волновое сопротивление контура;
Q=KU — качество, или добротность контура.
Возникновение резонанса напряжений в электрических цепях (сильно-точных) нежелательно. Чрезмерное повышение напряжений на ёмкостном и индуктивном элементах при резонансе может вывести их из строя.
В слаботочных (электронных, радиотехнических) цепях явление резонанса напряжений находит широкое применение. Благодаря усилению на реактивных элементах последовательной радиотехнической цепи (последовательный колебательный контур) при резонансе можно выделять напряжение, частота которого равна резонансной частоте цепи. Это позволяет осуществить прием и использование данного напряжения в системах радио-, телевизионного и радиолокационного приема.
ИССЛЕДОВАНИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ
КАТУШКИ ИНДУКТИВНОСТИ И КОНДЕНСАТОРА.
РЕЗОНАНС ТОКОВ. КОМПЕНСАЦИЯ РЕАКТИВНОЙ МОЩНОСТИ В ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА
Резонанс токов возникает в цепи синусоидального тока при параллельном включении ветвей, содержащих R, L и С (рисунок 3.1). Его можно трактовать как увеличение токов, текущих в ветвях (I1 и I2) по сравнению с током общей цепи I, т. е. при резонансе I1 » I2 и могут быть больше или даже значительно больше I (явление усиления по току).
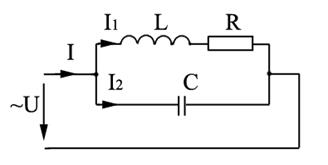
Рисунок 3.1
Исходя из первого закона Кирхгофа,
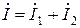 .
.
Для наглядности построим векторную диаграмму токов (рисунок 3.2).

Рисунок 3.2 — Векторная диаграмма токов
Вектор тока İ2 опережает вектор напряжения на 90°, а вектор тока İ1 отстает от вектора напряжения на угол
 .
.
При резонансе токов необходимо, чтобы
I1 = I1Р= I1sinj1 = I2,
где I1Р — реактивный ток в первой ветви.
Эти токи будут полностью компенсировать друг друга благодаря тому, что имеют разность фаз 180º, общий ток в неразветвленной части цепи совпадает по фазе с напряжением, т. е. становится чисто активным, угол j = 0, cosj = 1.
Аналитический расчет параллельных цепей переменного тока производится с помощью проводимостей. В данном случае общий ток цепи
I = Uy = U 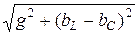 ,
,
где U — напряжение, приложенное к цепи, В;
y — полная проводимость цепи, 1/Ом = См (сименс);
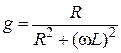 — активная проводимость ветви R, L;
— активная проводимость ветви R, L;
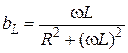 — индуктивная проводимость ветви R, L;
— индуктивная проводимость ветви R, L;
 — ёмкостная проводимость ветви с конденсатором.
— ёмкостная проводимость ветви с конденсатором.
Изменяя индуктивность L, ёмкость С, сопротивление R или частоту питающего напряжения, можно добиться того, что 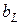 будет равняться
будет равняться 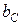 , и тогда общий ток I = Ug становится чисто активным. Это соответствует режиму резонанса. Следовательно, условие резонанса токов можно записать как
, и тогда общий ток I = Ug становится чисто активным. Это соответствует режиму резонанса. Следовательно, условие резонанса токов можно записать как 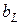 =
= 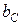 или
или

откуда резонансная частота
 ,
,
где  — резонансная частота параллельного контура;
— резонансная частота параллельного контура;
 — резонансная частота последовательного контура.
— резонансная частота последовательного контура.
В частном случае, когда можно пренебречь активным сопротивлением катушки индуктивности, условием резонанса становится равенство 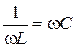 или
или  . В этом частном случае ток в неразветвленной части цепи равен нулю. Это значит, что притока энергии извне нет, но в замкнутом контуре, образуемом двумя ветвями, ток проходит. В этом контуре происходит непрерывное превращение энергии электрического поля, запасенного конденсатором, в энергию магнитного поля, запасенную катушкой, и обратно.
. В этом частном случае ток в неразветвленной части цепи равен нулю. Это значит, что притока энергии извне нет, но в замкнутом контуре, образуемом двумя ветвями, ток проходит. В этом контуре происходит непрерывное превращение энергии электрического поля, запасенного конденсатором, в энергию магнитного поля, запасенную катушкой, и обратно.
Для реального контура, обладающего активным сопротивлением R (сопротивление соединительных проводов, активное сопротивление катушки индуктивности 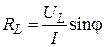 ), протекание тока будет сопровождаться кроме обратимого обмена энергией также необратимым преобразованием электрической энергии в другие виды энергии (тепловую, лучевую, механическую, химическую).
), протекание тока будет сопровождаться кроме обратимого обмена энергией также необратимым преобразованием электрической энергии в другие виды энергии (тепловую, лучевую, механическую, химическую).
С этими процессами напрямую связаны мощности цепи синусоидального тока, так как коэффициент мощности
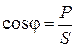 ,
,
где  — активная мощность, Вт;
— активная мощность, Вт;
 — полная мощность, ВА;
— полная мощность, ВА;
 — реактивная мощность, ВАр.
— реактивная мощность, ВАр.
Так как b = 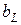 -
-  , то
, то  .
.
Наряду с понятием активной мощности Р и реактивной мощности Q применяется понятие полной мощности
S = UI.
Полная, активная и реактивная мощности образуют так называемый треугольник мощностей (рисунок 3.3).

Рисунок 3.3 — Треугольник мощностей
Как видно из треугольника мощностей, при снижении реактивной мощности до нуля полная мощность становится равна активной мощности, угол j уменьшается до нуля.
Для компенсации индуктивной составляющей реактивной мощности QL параллельно нагрузке включают конденсаторы. При этом, подбирая ёмкость конденсатора, можно добиться приближенной компенсации реактивной мощности потребителей электрической энергии, т. е. обеспечить QL- QС ® 0.
Повышение коэффициента мощности cosj используется в электроснабжении.
Большинство потребителей электроэнергии являются активно-индуктивной нагрузкой, что приводит к уменьшению коэффициента мощности. Параллельное подключение конденсатора приводит к уменьшению тока в подводящих проводах при неизменной активной мощности. При этом уменьшаются потери в линиях электропередач, которые пропорциональны квадрату тока:
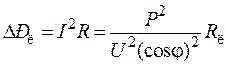 .
.
Аналогично снижаются потери в обмотках генераторов и трансформаторов, снабжающих электростанций и трансформаторных подстанций.
Ёмкость, необходимую для повышения коэффициента мощности до требуемого значения, можно определить по формуле:
С= 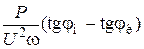 ,
,
где jн, jк — угол сдвига фаз между напряжением и током до компенсации и после компенсации соответственно;
 — активная мощность, потребляемая нагрузкой;
— активная мощность, потребляемая нагрузкой;
w=2pf — частота синусоидального тока.
1. Исследовать явление резонанса токов в цепи с параллельным соединением катушки индуктивности и конденсатора.
а) Ознакомиться с оборудованием рабочего места и измерительными приборами, используемыми при выполнении работы.
б) Собрать электрическую цепь согласно электрической схеме, представленной на рисунке 3.4.
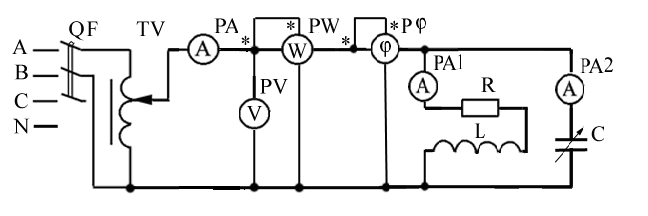
Рисунок 3.4 — Схема лабораторной установки
В данной электрической схеме использованы электроизмерительные приборы: РА – амперметр Э514 0÷1А;
PV – вольтметр Э365 0÷250 В;
Pj — фазометр ; PW — ваттметр;
РА1, РА2 – амперметры Э365 0÷2А.
в) При помощи лабораторного автотрансформатора (ЛАТр) установить на входе электрической цепи напряжение U = 100 В и поддерживать его во время опыта неизменным. Не производя записей результатов измерений, убедиться, что при изменении ёмкости конденсатора от нуля до наибольшего возможного значения общий ток сначала убывает, а затем начинает возрастать. Такое же изменение угла j будет при этом наблюдаться на фазометре. Эти явления свидетельствуют о возможности увеличения коэффициента мощности нагрузки, а следовательно, и коэффициента полезного действия цепи путем параллельного подключения конденсатора С к катушке индуктивности, используемой в виде нагрузки.
г) Изменяя соответствующими переключателями на лабораторном стенде величину ёмкости конденсатора исследуемой цепи от 5 мкФ до наибольшего ее значения, произвести не менее пяти измерений. При этом обязательно найти резонанс токов, до резонанса выполнить два измерения и после резонанса осуществить не менее двух измерений. Результаты измерений занести в таблицу 3.1.
Таблица 3.1
| Измерено | Вычислено | |||||||||||
| C, мкФ | U, В | I, A | I1, A | I2, A | j, | cosj | S, ВА | P, Вт | Q, ВАр | bC, 
| bL, 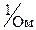
| g, 
|
2. Вычислить величины S, P, Q, bC, bL, g и результаты занести в таблицу 3.1.
При вычислениях можно использовать следующие формулы:
–полная мощность электрической цепи
S = UI;
– активная и реактивная мощности цепи
Р = UIcosj, Q = UIsinj ;
– реактивная составляющая проводимости ёмкостной ветви
bC =  ,
,
активной составляющей проводимости ёмкостной ветви можно практически пренебречь;
– реактивная составляющая проводимости индуктивной ветви bL и активная составляющая проводимости этой ветви g связаны между собой зависимостью:
 ,
,
где y1 — полная проводимость индуктивной ветви.
Отсюда 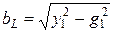 .
.
Значение полной проводимости индуктивной ветви y1 можно определить из очевидной зависимости: y1 =  .
.
Если учесть, что мы пренебрегали активной составляющей проводимости ёмкостной ветви и считаем имеющей активную составляющую проводимости только индуктивную ветвь, появляется возможность воспользоваться равенством:
 ,
,
где g — активная составляющая проводимости цепи двух параллельных ветвей.
Дальнейшее определение g1 не составляет труда, так как известно, что активная составляющая проводимости цепи и активная составляющая потребляемой мощности связаны зависимостью
Р = gU2.
Отсюда  .
.
3. Компенсация реактивной мощности.
а) Отключить конденсаторы, оставив в схеме только активно-индуктивную нагрузку.
б) При помощи лабораторного автотрансформатора (ЛАТр) установить на входе электрической цепи напряжение U = 100 В. Произвести измерения, необходимые для заполнения первой строки таблицы 3.2.
Таблица 3.2.
| Показания приборов и результаты вычислений | U, B | I, A | I1, A | I2, A | P, Вт | Q, ВАр | cosj | j | C, мкФ |
| Режим до компенсации | |||||||||
| После компенсации |
в) Вычислить реактивную мощность Q и значение ёмкости конденсатора С, необходимое для ее компенсации до уровня, указанного преподавателем.
г) Набрать на батарее конденсаторов необходимую ёмкость и произвести компенсацию реактивной мощности. Данные внести в таблицу 3.2.
Сравнить результаты измерений, полученные до и после компенсации (включения конденсатора в цепь). Сделать выводы.
4. По результатам проведенных исследований
а) построить векторные диаграммы токов и напряжения, отвечающих дорезонансному, резонансному и послерезонансному режимам цепи;
б) построить графики изменения I, I1, I2, cosj в зависимости от изменения ёмкости конденсатора С (построение всех графиков произвести в одной координатной системе);
в) построить векторные диаграммы и треугольники мощностей до и после компенсации реактивной мощности.
Дата добавления: 2020-10-14; просмотров: 547;











