Поверка приборов. Виды погрешностей
При любом измерении возможны погрешности, т.е. отклонения результатов измерений от истинного значения измеряемой величины, которые обуславливаются несовершенством измерительного механизма, влиянием внешних факторов (наличием магнитных и электрических полей, изменением магнитных и электрических полей, изменением температуры окружающей среды и т.д.), несовершенством органов чувств человека и другими случайными факторами.
Разность между показаниями прибора Ап и действительным значением измеряемой величины Ад, выраженная в единицах измеряемой величины, называется абсолютной погрешностью измерения.
DА= Ап- Ад.
Величина, обратная по знаку абсолютной погрешности, носит название поправки.
DР= -DА= Ад - Ап .
Для оценки точности произведенного измерения служит относительная погрешность d, которая представляет собой отношение абсолютной погрешности к истинному значению измеряемой величины, выраженное обычно в процентах:
d = 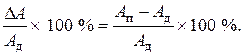
По относительной погрешности оценивать точность, например, стрелочных измерительных приборов неудобно, так как для них абсолютная погрешность вдоль всей шкалы практически постоянна, поэтому с уменьшением значения измеряемой величины растет относительная погрешность.
Точность измерительных приборов оценивают по приведенным погрешностям. Приведенная погрешность — это отношение абсолютной погрешности измерения к диапазону измерений устройства (или к предельному значению), выраженное в процентах:
g =  ,
,
где Ап — показания прибора; Ад — действительное значение измеряемой величины; Ан — предельное значение измерительного прибора.
По максимальному значению приведенной погрешности (основному значению) определяют класс точности прибора. Их восемь: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4. Класс точности указывается на шкале прибора.
При эксплуатации приборов периодически необходимо поверять их погрешности. Поверки в обязательном порядке должны проводиться после ремонтов и регулировки.
Поверка измерительного прибора должна включать его внешний осмотр, определение погрешности и документальное оформление поверки.
Электроизмерительные приборы классов точности 0,5; 1,0; 1,5; 2,5; 4 поверяются по методу сравнения их показаний с показанием образцовых приборов. При этом: а) допустимая погрешность (класс точности) образцового прибора должна быть не менее чем в 3 раза меньше допустимой погрешности поверяемого прибора; б) верхний предел измерения образцового прибора должен быть таким же, как у поверяемого, или не превышать его более чем на 25 %.
Поверка приборов осуществляется для всех оцифрованных точек шкалы при возрастании и убывании измеряемой величины.
Основная погрешность приборов определяется как наибольшая из всех погрешностей, найденных при монотонном увеличении и уменьшении измеряемой величины.
Поверка амперметра
Для поверки амперметра необходимо:
1. Собрать цепь по схеме (рисунок 1.5), используя приборы и элементы лабораторного стенда.
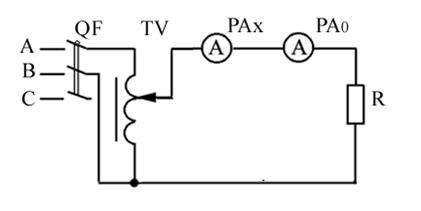
Рисунок 1.5 — Схема поверки амперметра
На рисунке 1.5 РАx — поверяемый амперметр (по указанию преподавателя); РА0 — образцовый прибор (прибор, который необходимо подобрать); R — резистор; TV — лабораторный автотрансформатор (ЛАТр); QF — авто-матический выключатель;
2. Убедиться, что движок ЛАТра установлен в положение, соответствующее минимальному значению напряжения на выходе, подать напряжение на цепь;
3. Меняя напряжение, подаваемое на электрическую цепь с помощью ЛАТра, произвести поверку амперметра на всех оцифрованных точках его шкалы (0; 0,2; 0,4; 0,6; 0,8; 1,0 А) при возрастании и убывании измеряемой величины;
4. Результаты измерений и вычислений занести в таблицу 1.1.
В таблице I0, I0¯— показания образцового прибора при изменении питающего напряжения вверх и вниз соответственно; I0ср — среднее значение показания образцового прибора
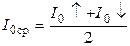 ;
;
Таблица 1.1
| № п/п | Измерено | Вычислено | |||||||
| Ix, A | I0, A | I0¯, A | I0ср, A | DI, А | DР, А | d,% | g,% | ||
| 1. | |||||||||
| 2. | 0,2 | ||||||||
| 3. | 0,4 | ||||||||
| 4. | 0,6 | ||||||||
| 5. | 0,8 | ||||||||
| 6. | 1,0 | ||||||||
5. По результатам измерений определить погрешности поверяемого амперметра и дать заключение о его классе точности.
Поверка вольтметра
1. Собрать схему согласно рисунку 1.6 на лабораторном стенде.
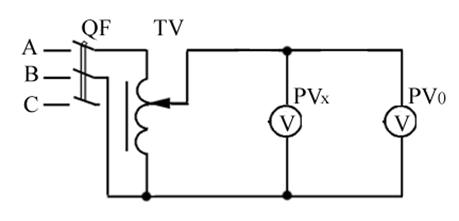
Рисунок 1.6 — Схема поверки вольтметра
На рисунке 1.6 РVx — поверяемый вольтметр; РV0 — образцовый вольтметр, который необходимо подобрать.
2. Убедиться, что движок ЛАТра установлен в положение, соответствующее минимальному значению напряжения на выходе, подать напряжение на цепь.
3. Меняя напряжение, подаваемое на электрическую цепь с помощью ЛАТра, произвести поверку вольтметра на всех оцифрованных точках его шкалы при возрастании и убывании измеряемой величины.
4. Результаты измерений и вычислений занести в таблицу 1.2.
Таблица 1.2
| № п/п | Измерено | Вычислено | ||||||
| Ux, В | U0,В | U0¯,В | U0ср, В | DU, В | DР, В | d,% | g,% | |
| 1. | ||||||||
| 2. | ||||||||
| 3. | ||||||||
| 4. | ||||||||
| 5. | ||||||||
| 6. |
В таблице U0, U0¯— показания образцового прибора при изменении питающего напряжения вверх и вниз соответственно; U0ср — среднее значение показания образцового вольтметра.
5. По результатам измерений определить погрешности поверяемого вольтметра и сделать вывод о его соответствии своему классу точности.
ИССЛЕДОВАНИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ
КАТУШКИ ИНДУКТИВНОСТИ И КОНДЕНСАТОРА.
Схема электрической цепи с последовательным соединением активного, индуктивного и ёмкостного сопротивлений представлена на рисунке 2.1, на котором R — активное сопротивление; L — индуктивность катушки индуктивности; С — ёмкость конденсатора; UR, UL, UC — падения напряжений на активном, индуктивном и ёмкостном сопротивлениях; U — напряжение питания на зажимах цепи; I — ток в цепи.
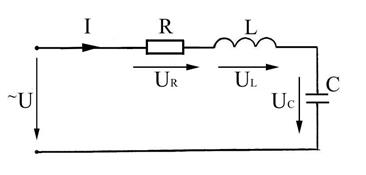
Рисунок 2.1 — Последовательное соединение элементов R, L и С
В соответствии с законом Ома, связь между током и напряжением для действующих значений можно представить выражением:
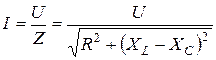 ,
,
где 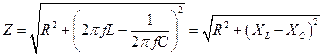 — полное сопротивление цепи; R, XL, XC — соответственно активная, индуктивная и ёмкостная составляющие полного сопротивления цепи.
— полное сопротивление цепи; R, XL, XC — соответственно активная, индуктивная и ёмкостная составляющие полного сопротивления цепи.
В комплексной форме закон Ома можно представить выражением:
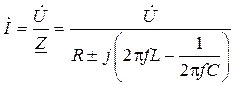 ,
,
где 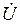 — комплекс действующего значения напряжения на входе цепи;
— комплекс действующего значения напряжения на входе цепи; 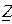 — комплекс полного сопротивления цепи.
— комплекс полного сопротивления цепи.
Индуктивное и ёмкостное сопротивления цепи зависят не только от физических параметров катушки и конденсатора, а также и от частоты питающего напряжения f.
Эта зависимость определяется выражениями:
ХL = wL = 2pfL , XC = 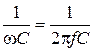 .
.
Приложенное к рассматриваемой электрической цепи питающее напряжение U уравновешивается падением напряжения на отдельных ее участках.
Согласно второму закону Кирхгофа, этому положению соответствует равенство:
 ,
,
где 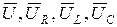 — векторы действующих значений приложенного к цепи напряжения на активном, индуктивном и ёмкостном элементах соответственно.
— векторы действующих значений приложенного к цепи напряжения на активном, индуктивном и ёмкостном элементах соответственно.
Следует обратить внимание, что законы Кирхгофа записываются в комплексной или векторной форме, т. е. 2-ой закон Кирхгофа можно записать в виде:
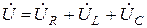 .
.
Векторная диаграмма для рассматриваемой цепи, из которой можно выделить треугольник напряжений аbс представлена на рисунке 2.2.
Гипотенуза треугольника напряжений соответствует действующему значению приложенного к цепи напряжения U, а катеты — активной и реактивной составляющим этого напряжения.
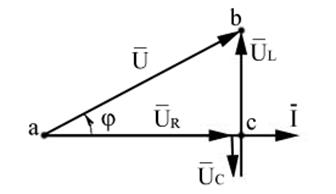
Рисунок 2.2 —Треугольник напряжений
Угол между векторами напряжения и тока j называется углом сдвига фаз и определяется разностью начальных фаз напряжения и тока, т. е. j = yu - yi.
Разделив величины длин сторон треугольника напряжений на число, равное действующему значению тока в рассматриваемой цепи, получим треугольник, у которого стороны будут в масштабе соответствовать значениям сопротивлений этой цепи. Этот треугольник называется треугольником сопротивлений (рисунок 2.3.).
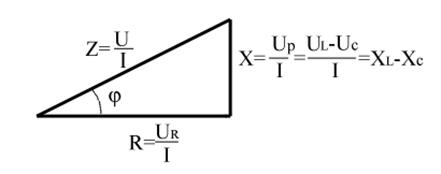
Рисунок 2.3 — Треугольник сопротивлений
Гипотенуза треугольника сопротивлений соответствует в масштабе полному сопротивлению цепи Z, а катеты — его активной R и реактивной Х составляющим.
Значение j зависит от соотношения активного и реактивного сопротивлений цепи. Из треугольника сопротивлений угол сдвига фаз можно определить как
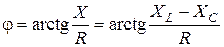 .
.
В зависимости от соотношения Х и R могут иметь место три характерных режима работы цепи:
1) активно-индуктивный, когда ХL>XC, j > 0 (рисунок 2.4);
2) активно-ёмкостной, при котором ХL<XC, j <0 (рисунок 2.6);
3) активный, при котором ХL=XC, j = 0, т. е. ток и напряжение совпадают по фазе (рисунок 2.5).
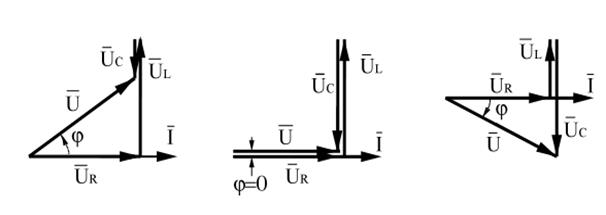
Рисунок 2.4 Рисунок 2.5 Рисунок 2.6
Режим отставания по фазе тока от напряжения имеет место при положительных Up, когда индуктивная составляющая напряжения больше активной составляющей: UL>UC. Последнее обеспечивается, если ХL>XC.
Режим, при котором ток опережает по фазе приложенное напряжение, имеет место при условии UL<UC и, соответственно, при ХL<XC.
При ХL=XC, также UL=UC, и при этом также возможен резонанс напря-жений, основным проявлением которого можно назвать резкое увеличение величин напряжения на реактивных элементах цепи (усиление по напряже-нию).
Дата добавления: 2020-10-14; просмотров: 409;











