ЛЕКЦИЯ 8. ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Нагрузкой электрических цепей в общем случае являются электромагнитные устройства. Их работа основана на использовании энергии электрического и магнитного поля. К электромагнитным устройствам относятся трансформаторы, генераторы, электродвигатели, преобразователи, электроизмерительные приборы, реле, муфты и другие.
Чтобы понять принципы построения и работы таких устройств, усвоить методы их расчета, необходимо изучить теорию магнитного поля. В рамках курса лекций рассмотрим ее основы.
1. ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ И СООТНОШЕНИЯ
Основные физические величины, описывающие магнитное поле, известны из курса физики. К ним относятся магнитная индукция, магнитный поток, намагниченность, напряженность магнитного поля, магнитная проницаемость.
Магнитная индукция В определяется силой, испытываемой единичным зарядом Q, движущимся в магнитном поле со скоростью V:
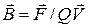 . (8.1)
. (8.1)
Магнитная индукция измеряется в теслах [Тл].
Магнитный поток  - это поток вектора магнитной индукции через площадь S:
- это поток вектора магнитной индукции через площадь S:
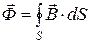 . (8.2)
. (8.2)
В однородном магнитном поле, перпендикулярном площади S, магнитный поток можно определить произведением скалярных величин:
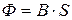 . (8.3)
. (8.3)
Магнитный поток измеряется в веберах [Вб]:
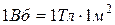 .
.
Намагниченность есть магнитный момент единицы объема вещества:
 , (8.4)
, (8.4)
где  - вектор магнитного момента элементарного контура:
- вектор магнитного момента элементарного контура:
Напряженность магнитного поля Н связана с магнитной индукцией В и намагниченностью М зависимостью:
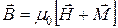 , (8.5)
, (8.5)
где 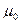 - магнитная постоянная, причем,
- магнитная постоянная, причем, 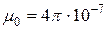 Гн/м.
Гн/м.
Намагниченность и напряженность магнитного поля измеряются в А/м.
Для магнитного поля в ферромагнитной среде связь между магнитной индукцией и напряженностью поля определяется выражением:
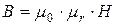 , (8.6)
, (8.6)
где 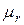 - относительная магнитная проницаемость.
- относительная магнитная проницаемость.
О наличии магнитного поля судят по воздействию, которое оно оказывает на помещенные в него тела. Различают индукционное и электромеханическое воздействия.
Индукционное воздействие магнитного поля состоит в том, что при перемещении проводника в постоянном магнитном поле в проводнике наводится электродвижущая сила. Если же это поле переменное, то Э.Д.С. возникает в неподвижном проводнике. На индукционном действии магнитного поля основана работа таких электромагнитных устройств, как трансформаторы, электрические генераторы, электроизмерительные приборы и др.
Электромеханическое воздействие магнитного поля заключается в том, что на проводник с током в магнитном поле действует сила со стороны поля. На электромеханическом действии магнитного поля основана работа электрических двигателей, реле, электромагнитных муфт и др. устройств.
2. ХАРАКТЕРИСТИКА МАГНИТНЫХ СВОЙСТВ
ФЕРРОМАГНИТНЫХ МАТЕРИАЛОВ
Ферромагнитные материалы характеризуют зависимостью магнитной индукции от напряженности магнитного поля:
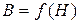 .
.
Эта зависимость устанавливается опытным путем. На рис. 8.1. приведено ферромагнитное кольцо с обмоткой в виде витков провода. Если
увеличивать ток в витках, то Н и В будут возрастать от нулевых значений по кривой начальной намагниченности (рис.8.2). Участок «оа» кривой есть начальная область, «аб» - область интенсивного намагничивания, «бв» - колено кривой, «вг» - участок насыщения, на котором намагниченность практически постоянная.
Отношение 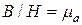 называется абсолютной магнитной проницаемостью, причем,
называется абсолютной магнитной проницаемостью, причем,
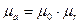 ,
,
где 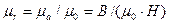 - относительная магнитная проницаемость.
- относительная магнитная проницаемость.

Относительная магнитная проницаемость 
 зависит от Н и может изменяться от единиц до десятков тысяч. Она показывает, во сколько раз магнитная проницаемость материала больше магнитной проницаемости вакуума.
зависит от Н и может изменяться от единиц до десятков тысяч. Она показывает, во сколько раз магнитная проницаемость материала больше магнитной проницаемости вакуума.
Намагничивание сопровождается отставанием изменения вектора 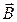 от вектора
от вектора 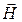 . Это обусловлено внутренним трением между границами областей самопроизвольного намагничивания и потерей энергии. Поэтому при циклическом изменении Н зависимость В=f(H) приобретает вид петли гистерезиса (рис.8.3). На рисунке Вr - остаточная намагниченность, НС - коэрцитивная сила. Площадь петли гистерезиса пропорциональна энергии, выделяющейся в единице объема ферромагнитного материала за один цикл перемагничивания.
. Это обусловлено внутренним трением между границами областей самопроизвольного намагничивания и потерей энергии. Поэтому при циклическом изменении Н зависимость В=f(H) приобретает вид петли гистерезиса (рис.8.3). На рисунке Вr - остаточная намагниченность, НС - коэрцитивная сила. Площадь петли гистерезиса пропорциональна энергии, выделяющейся в единице объема ферромагнитного материала за один цикл перемагничивания.
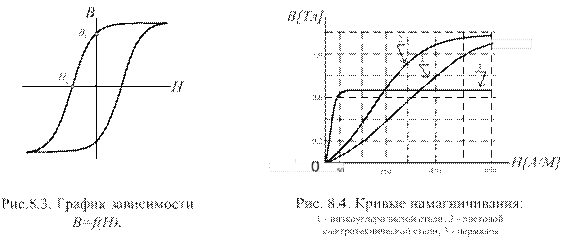
Ферромагнитные материалы бывают магнитотвердые и магнитомягкие. Магнитомягкие используются для изготовления магнитопроводов. К таким материалам относятся:
-технически чистое железо (низкоуглеродистые стали),
-листовая электротехническая сталь (железокремнистая),
-железоникелевые стали (пермаллой).
Кривые намагничивания этих материалов приведены на рис.8.4. Графики кривых начального намагничивания используется для выбора
материалов при расчете электромагнитных устройств.
3. МАГНИТНЫЕ ЦЕПИ
Практическим результатом теории магнитного поля является математический аппарат и методы расчета электромагнитных устройств. Любое электромагнитное устройство состоит из намагничивающих элементов (намагничивающих катушек, постоянных магнитов) и магнитопровода. Расчет заключается в определении материалов и геометрических размеров магнитопровода, тока катушки, числа ее витков и ее размеров.
Намагничивающая катушка создает магнитное поле в магнитопроводе и в окружающем пространстве. Так как 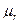 ферромагнитных материалов много больше
ферромагнитных материалов много больше 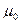 , то основная часть линий магнитного поля проходит по магнитопроводу. Совокупность ферромагнитных тел и сред, по которым замыкается магнитный поток, называется магнитной цепью.
, то основная часть линий магнитного поля проходит по магнитопроводу. Совокупность ферромагнитных тел и сред, по которым замыкается магнитный поток, называется магнитной цепью.
При анализе магнитных цепей допускаются следующие упрощения:
1. Магнитное поле изображается распределением магнитных силовых линий в магнитопроводе. Если поле равномерно распределено по сечению
магнитопровода, то его изображают параллельными линиями.
2.Магнитная индукция и напряженность считаются равномерно распределенными по объему магнитопровода.
3.Магнитный поток считается сосредоточенным только в магнитопроводе.
Магнитные цепи делятся на однородные и неоднородные, разветвленные и неразветвленные, симметричные и несимметричные.
Однородная неразветвленная магнитная цепь приведена на рис.8.1. Это замкнутый магнитопровод с равномерной обмоткой. Каждый виток обмотки создает линии магнитной индукции, которые замыкаются по магнитопроводу. Совокупность витков создает общий магнитный поток.
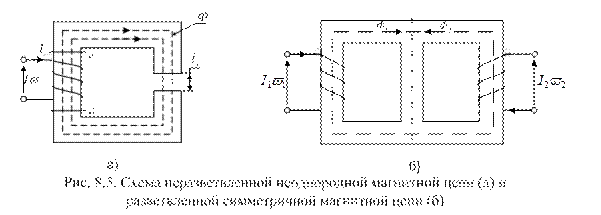
На практике широко применяются неоднородные магнитные цепи. В таких цепях обмотка сосредоточена в одном месте, а магнитопровод имеет участки с различной магнитной проницаемостью 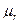 (например, участок с воздушным зазором lз, рис. 8.5, а).
(например, участок с воздушным зазором lз, рис. 8.5, а).
С учетом перечисленных упрощений считается, что весь магнитный поток Ф проходит по магнитопроводу. Он одинаков как в ферромагнитном материале, так и в воздушном зазоре. Площадь воздушного зазора принимается равной площади сечения ферромагнитного материала 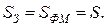 Так как магнитная индукция В = Ф/S, то видим, что онаодинакова в любой точке магнитопровода. Однако напряженность магнитного поля Н в ферромагнитном материале и воздушном зазоре различна, поэтому такая цепь называется неоднородной.
Так как магнитная индукция В = Ф/S, то видим, что онаодинакова в любой точке магнитопровода. Однако напряженность магнитного поля Н в ферромагнитном материале и воздушном зазоре различна, поэтому такая цепь называется неоднородной.
Примерами разветвленных магнитных цепей могут служить цепи электрических машин, трансформаторов, поляризованных реле. Пример одной из таких цепей приведен на рис. 8.5, б. Магнитная цепь на рис. 8.5, б симметрична, если в ней Ф1 = Ф2, обе ее части справа и слева от штрих- пунктирной линии одинаковы в геометрическом отношении и изготовлены из одного материала, а I1 = I2; 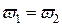 . Достаточно изменить один из перечисленных параметров или изменить направление одного из токов, чтобы цепь стала несимметричной.
. Достаточно изменить один из перечисленных параметров или изменить направление одного из токов, чтобы цепь стала несимметричной.
Суть анализа магнитных цепей сводится к определению их основных параметров: магнитного потока Ф, напряженности магнитного поля Н, магнитной индукции В, сечения магнитопровода S, тока катушки I и др. При этом пользуются понятиями магнитодвижущей силы, закона полного тока, магнитного напряжения 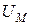 и магнитного сопротивления
и магнитного сопротивления 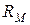 .
.
Если по намагничивающей обмотке протекает ток I, то магнитодвижущей силой обмотки F называют произведение величины тока на число витков:
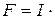 v. (8.7)
v. (8.7)
Связь между магнитодвижущей силой F и напряженностью магнитного поля Н устанавливает закон полного тока:
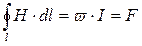 . (8.8)
. (8.8)
При анализе магнитных цепей пользуются значением средней линии магнитопровода, поэтому:
 . (8.9)
. (8.9)
Выделим в магнитопроводе рис. 8.5, а участок длиной «аб».
Произведение
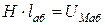 (8.10)
(8.10)
называют магнитным напряжением.
Если магнитная цепь содержит два неоднородных участка длиной 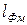 и
и  , то
, то

или:
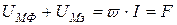 . (8.11)
. (8.11)
Таким образом, алгебраическая сумма магнитных напряжений на участках цепи равна магнитодвижущей силе обмотки. Выражение (8.11) представляет собой второй закон Кирхгофа для магнитной цепи.
Аналогом первого закона Кирхгофа является теорема Гаусса: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

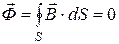 . (8.12)
. (8.12)
Определим выражение для магнитного сопротивления. Для этого преобразуем (8.10) и выделим множитель, определяемый только параметрами цепи:
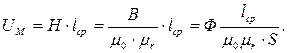
Обозначим выражение:
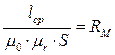 [Гн -1],
[Гн -1],
где 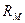 - магнитное сопротивление.
- магнитное сопротивление.
Тогда
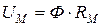 , [А]. (8.13)
, [А]. (8.13)
Равенство (8.13) представляет собой закон Ома для магнитной цепи.
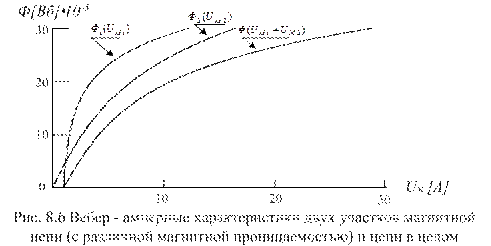
Если основной характеристикой электрической цепи является вольтамперная характеристика, то для магнитной цепи - это вебер-амперная характеристика - зависимость магнитного потока от падения магнитного напряжения, т.е. 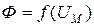 , рис.3.6. Вебер-амперные характеристики часто применяют для анализа сложных магнитных цепей. Рис. 8.6 демонстрирует возможности такого применения. На нем вебер-амперная характеристика сложной магнитной цепи, состоящей из участков с различной магнитной проницаемостью µ1 и µ2, построена сложением ординат вебер-амперных характеристик этих участков.
, рис.3.6. Вебер-амперные характеристики часто применяют для анализа сложных магнитных цепей. Рис. 8.6 демонстрирует возможности такого применения. На нем вебер-амперная характеристика сложной магнитной цепи, состоящей из участков с различной магнитной проницаемостью µ1 и µ2, построена сложением ординат вебер-амперных характеристик этих участков.
Вебер-амперные характеристики адекватны гистерезисным – 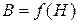 , так как магнитный поток Ф прямо пропорционален магнитной индукции (8.3), а падения магнитного напряжения – напряженности магнитного поля Н:
, так как магнитный поток Ф прямо пропорционален магнитной индукции (8.3), а падения магнитного напряжения – напряженности магнитного поля Н:
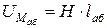 .
.
Вебер-амперные характеристики в готовом виде не задаются. Перед расчетом магнитных цепей их надо построить с помощью кривых начальной намагниченности ферромагнитных материалов, входящих в магнитную
цепь. Порядок построения вебер-амперной характеристики рассмотрим на
примере магнитной цепи, приведенной на рисунке 8.7, а.
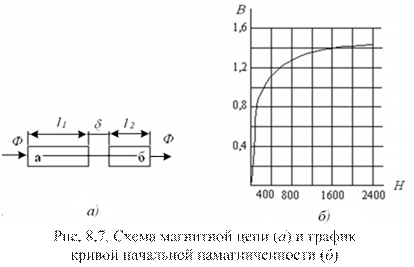
Пусть участки 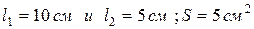 выполнены из ферромагнитного материала, кривая
выполнены из ферромагнитного материала, кривая 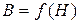 которого приведена на рис. 8.7, б. Участок δ – воздушный зазор длиной δ = 0,005 см. Требуется построить вебер-амперную характеристику участка цепи между точками «а» и «б».
которого приведена на рис. 8.7, б. Участок δ – воздушный зазор длиной δ = 0,005 см. Требуется построить вебер-амперную характеристику участка цепи между точками «а» и «б».
Порядок построения:
1. При построении учитываем введенные упрощения, в частности, о том, что 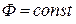 по всей длине магнитопровода от «а» до «б».
по всей длине магнитопровода от «а» до «б».
2. Считаем, что сечение воздушного зазора равно сечению участков l1 и l2.
3. Задаемся рядом произвольных значений магнитной индукции:
В = : 0; 0,5; 0,8; 1,0; 1,1; 1,2; 1,3; 1,4 Тл.
По формуле Ф = В∙S рассчитываем соответствующие значения магнитного потока:
Ф = : 0,25 ∙ 10-5; 40 ∙ 10-5; 50 ∙ 10-5; 55 ∙ 10-5; 60 10-5; 65 ∙ 10-5; 70 ∙ 10-5 Вб.
4. По каждому из заданных значений В, для участков из ферромагнитного материала – l1 и l2, находим Н по графику рис. 8.7, б. Например, для
В = 0,5 Тл Н1 = Н2 = 40 (А/м).
Для
В = 0,8 Тл Н1 = Н2 = 130 (А/м).
5. Для воздушного зазора рассчитываем Нδ:
 (А/м).
(А/м).
6. Определяем падение магнитного напряжения между точками «а» и «б» – UМаб:
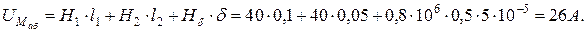
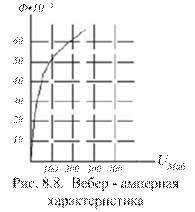
Подобные расчеты проводим для каждого из выбранных значений В. По
результатам расчетов строим график Ф = f(UМ) (см. рис. 8.8).
Подводя итог рассмотренным вопросам, отметим, что магнитный поток в магнитной цепи – это аналог тока в электрической цепи. Магнитодвижущая сила – аналог ЭДС. Как и электрические цепи, магнитные цепи характеризуются магнитным сопротивлением, подчиняются законам Ома и Кирхгофа в трактовке магнитных цепей.
Вебер-амперная характеристика участка магнитной цепи является аналогом вольтамперной характеристики нелинейного элемента (НЭ) электрической цепи. Поэтому методы и приемы расчета электрических цепей с НЭ приемлемы и к расчету магнитных цепей. Одним из таких методов явля-ется метод двух узлов.
4. АНАЛИЗ РАЗВЕТВЛЕННОЙ МАГНИТНОЙ ЦЕПИ МЕТОДОМ
ДВУХ УЗЛОВ.
Метод применим к магнитным цепям с параллельными участками магнитопровода – ветвями. Пример такой цепи приведен на рис. 8.9. Это разветвленная неоднородная магнитная цепь с тремя параллельными ветвями. Условно выбранные положительные направления магнитных потоков

показаны на рис. стрелками. В каждой ветви создается падение магнитного напряжения: UМ1, UМ2, UМ3, поэтому для каждой ветви может быть построена своя вебер – амперная характеристика:
Ф1 = f(UМ1); Ф2 = f(UМ2); Ф3 = f(UМ3),(8.14)
где: UМ1 = H1∙l1 + Hδ∙lδ, UМ2 = H2∙l2+Hδ∙lδ, UМ3 = H3∙l3.
Пример вебер – амперных характеристик ветвей приведен на рис.8.10.
Выражения (8.14) позволяют определить магнитные потоки ветвей, но они не учитывают действующих в первой и второй ветвях цепи магнитодвижущих сил – 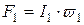 и
и  Этот недостаток можно устранить, если учесть, что структура цепи рис. 8.9 аналогична электрической
Этот недостаток можно устранить, если учесть, что структура цепи рис. 8.9 аналогична электрической
цепи с параллельно соединенными элементами.
Как и в электрической, в магнитной цепи можно выделить два узла – а и б, между которыми действует одинаковое для всех ветвей магнитное напряжение UМаб. Междуузловое магнитное напряжение UМаб определяется как падением магнитного напряжения, так и магнитодвижущей силой каждой ветви.
Если известно UМаб, то вебер – амперные характеристики всех ветвей можно выразить как функцию одной переменной:
Ф1 = f(UМаб); Ф2 = f(UМаб); Ф3 = f(UМаб).
Пример таких характеристик приведен на рис. 8.11, а. Суммируя ординаты характеристик, достаточно просто построить эквивалентную вебер – амперную характеристику всей цепи (рис. 8.11, б), а по ней определить искомые магнитные потоки всех ветвей. В этом и заключается основная суть рассматриваемого метода.
Рассмотрим алгоритм метода более подробно. Допустим, что анализу
подлежит магнитная цепь рис. 8.9. Пусть в этой цепи известны геометрические размеры, токи I1 и I2, число витков обмоток 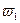 , и
, и 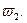 Кривая начального намагничивания ферромагнитного материала магнитопровода приведена на рис. 8.7, б. В результате анализа необходимо определить магнитные потоки в ветвях цепи.
Кривая начального намагничивания ферромагнитного материала магнитопровода приведена на рис. 8.7, б. В результате анализа необходимо определить магнитные потоки в ветвях цепи.
Последовательность анализа:
1. Обозначим узловые точки цепи индексами а и б.
2. Выберем положительное направление токов Ф1; Ф2; Ф3 от узла б к узлу а.
3. Используя график рис. 8.7, б, построим вебер-амперные характеристики ветвей цепи по (8.14). Характеристики приведены на рис. 8.10, а, б, в.
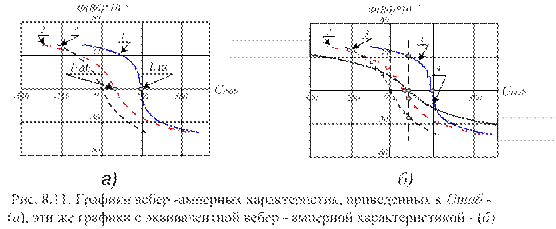
4. Выразим все магнитные потоки в функции одного переменного - 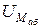 . Для этого учтем, что для первой ветви
. Для этого учтем, что для первой ветви
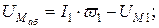
для второй ветви
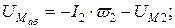
для третьей ветви
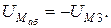
5. Построим графики 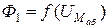 ,
,  и
и 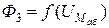 . Порядок построения графиков следующий:
. Порядок построения графиков следующий:
А. На оси Umаб откладываем точки по значениям 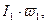
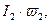
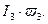
Б. На выделенные точки соответственно переносим начала координат графиков рис. 8.10, а, б, в.
В. Из заданных точек воспроизводим графики в зеркальном отобра-жении.
6. График эквивалентной вебер – амперной характеристики (кривая 4 рис. 8.11, б) строим, суммируя ординаты кривых 1, 2, 3. Точка пересечения эквивалентной вебер – амперной характеристики с осью абсцисс дает значение Umаб, при котором Ф1 = Ф2 = Ф3 = 0. Восстановим в этой точке перпендикуляр к оси абсцисс. Ординаты точек пересечения перпендикуляра с кривыми 1, 2 и 3 дадут соответственно значения магнитных потоков Ф1, Ф2 и Ф3 по величине и знаку.
5. ОСОБЕННОСТИ ФИЗИЧЕСКИХ ПРОЦЕССОВ В МАГНИТНЫХ
ЦЕПЯХ ПЕРЕМЕННОГО ТОКА
При анализе магнитных цепей переменного тока вводят следующие допущения:
1) магнитное поле рассеяния отсутствует;
2) активное сопротивление обмотки равно нулю.
При таких допущениях можно записать
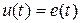 ,
,
где 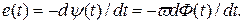
Отсюда следует, что магнитный поток в магнитопроводе переменный
и определяется напряжением (воздействием). Если 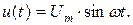 , то
, то
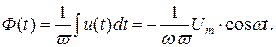 (8.15)
(8.15)
Таким образом, видим, что закон изменения магнитного потока Ф(t) определяется входным напряжением и не зависит от параметров цепи.
Фаза магнитного потока отстает от фазы напряжения на π/2. Это первая
особенность магнитных цепей переменного тока.
Чтобы определить вторую особенность, обратимся к известному для электрических цепей выражению
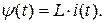
Из него следует, что
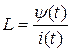 . (8.16)
. (8.16)
Подчеркнем, что выражение (8.16) справедливо для линейных электрических цепей. В таких цепях переменные ψ(t) и i(t) – линейные. В простейшей магнитной цепи для этих переменных установлены следующие соотношения:
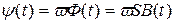 ;
;
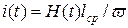 .
.
Переменные В(t) и Н(t) связаны по закону динамической петли гистерезиса. Эта связь нелинейна. Значит, для магнитных цепей зависимость (8.16) тоже нелинейна и должна иметь вид:
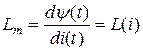 .
.
Следовательно, индуктивность обмотки магнитопровода зависит от тока и переменна. Это вторая особенность.
Теперь напряжение на участке магнитной цепи определится выражением
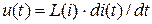 .
.
Видим, что 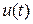 нелинейно. Отсюда третья особенность: магнитные цепи переменного тока являются нелинейными цепями, поэтому при синусоидальном напряжении на обмотке ток в ней оказывается несинусоидальным.
нелинейно. Отсюда третья особенность: магнитные цепи переменного тока являются нелинейными цепями, поэтому при синусоидальном напряжении на обмотке ток в ней оказывается несинусоидальным.
Изменение магнитного потока Ф(t) c частотой w приводит к нагреву
магнитопровода из-за гистерезиса. Следовательно, в магнитопроводе возникают потери электроэнергии. Их называют магнитными потерями. В магнитных цепях постоянного тока магнитных потерь нет. Это четвертая особенность физических процессов в магнитных цепях переменного тока.
КОНТРОЛЬНЫЕ ВОПРОСЫ
8.1. Приведите соотношения для основных физических величин магнитного поля.
8.2. Сформулируйте понятие относительной магнитной проницаемости. Приведите выражение для его определения.
8.3. Чем отличаются магнитомягкие ферромагнитные материалы от магнитотвердых материалов?
8.4. Что называют кривой начального намагничивания?
8.5. Поясните физическую сущность зависимости B = f(H) при циклическом изменении Н.
8.6. Из каких материалов конструируют магнитопроводы электромагнитных устройств и почему?
8.7. Приведите определение магнитной цепи. Назовите признаки однородных и неоднородных, разветвленных и неразветвленных, симметричных и несимметричных магнитных цепей.
8.8. В чем заключается отличие идеальной магнитной цепи от реальной?
8.9. Какой закон устанавливает пропорциональную зависимость между током намагничивающей обмотки и напряженностью магнитного поля в магнитопроводе магнитной цепи?
8.10. Приведите соотношения для магнитного напряжения UМ. магнитного сопротивления RМ, законов Кирхгофа и закона Ома в трактовке магнитных цепей.
8.11. Существует ли связь между вебер – амперной характеристикой магнитной цепи и кривой начального намагничивания?
8.12. В чем заключается суть метода двух узлов при анализе магнитных цепей?
8.13. Чем определяется закон изменения магнитного потока в магнитопроводе?
8.14. Почему напряжение на обмотке магнитопровода не пропорционально скорости изменения тока?
8.15. Почему магнитопровод нагревается при периодическом изменении напряженности магнитного поля?
Дата добавления: 2020-10-14; просмотров: 734;











