ЛЕКЦИЯ 10. ТРАНСФОРМАТОРЫ

1. ОБЩИЕ СВЕДЕНИЯ О ТРАНСФОРМАТОРАХ

Для практических целей трансформатор впервые был применен в 1876 году П.Н. Яблочковым. Он использовался в цепи питания электрических свечей. Широкое применение трансформаторы получили после того, как М.О. Доливо-Добровольским была предложена трехфазная система передачи электроэнергии и разработана конструкция первого трехфазного

трансформатора (1891г.).

Под трансформатором понимают статическое (т.е. без движущихся частей) электромагнитное устройство, предназначенное для преобразования переменного напряжения одной величины в переменное напряжение другой величины, но той же частоты.

Трансформатор состоит из двух и более обмоток, электрически изолированных друг от друга и охваченных общим магнитным потоком (рис. 10.1). Для усиления индуктивной связи между обмотками они размещаются на магнитопроводе. Передача энергии от источника к нагрузке происходит посредством переменного магнитного поля в магнитопроводе.

Магнитопроводы трансформаторов, предназначенных для работы в области низких частот, выполняют двух типов: пакетные и спиральные. Пакетные магнитопроводы состоят из тонких пластин ферромагнитного материала кольцевой, П или Ш- образной формы. Спиральные магнитопроводы изготавливают из тонкой ферромагнитной ленты в виде туго навитой часовой пружины. Пластины и отдельные витки спирали изолируют друг от друга лаком, жидким стеклом и т.п. веществами и запекают. Для уменьшения вихревых токов, магнитопроводы собирают из листовой электротехнической стали.

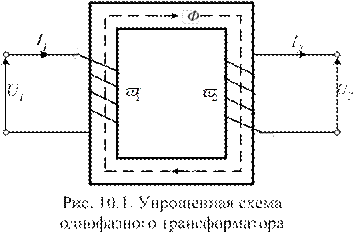
Под воздействием переменного тока в магнитопроводе возникает переменный магнитный поток Ф(t). В плоскости листа, перпендикулярной магнитному потоку, наводится Э.Д.С., которая вызывает ток, называемый вихревым. Вихревые токи по закону Ленца стремятся создать поток, встречный основному, что равноценно потерям энергии.

Потери на гистерезис и вихревые токи 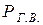пропорциональны действующему значению приложенного к индуктивности напряжения

и обратнопропорциональны сопротивлению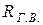

.

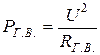Для уменьшения потерь увеличивают 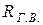. В этих целях сердечник изготавливают из тонких листов высококачественного магнитомягкого материала. Часто потери на гистерезис и вихревые токи объединяют и называют потерями в стали – Р_С.

Обмотка трансформатора, соединенная с источником питания, назы-вается первичной. Все величины, относящиеся к этой обмотке: число витков, напряжение, ток и т.д., – также именуются первичными. Их буквенные обозначения снабжаются индексом 1, например, 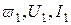(здесь применяются обозначения действующих значений тока и напряжения). Обмотка, к которой подключается нагрузка (потребитель электроэнергии) и относящиеся к ней величины, называются вторичными. Они снабжаются индексом 2.

Различают однофазные (для цепей однофазного тока) и трехфазные (для трехфазных цепей) трансформаторы. У трехфазного трансформатора первичной или вторичной обмоткой принято называть соответственно совокупность трех фазных обмоток одного напряжения.

Основные условные графические обозначения однофазного (а, б) и

трехфазного (в, г) трансформаторов показаны на рис. 10.2.

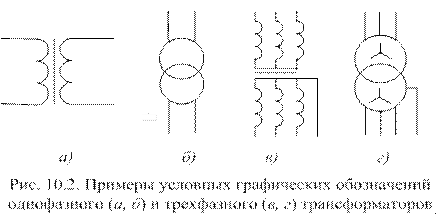
На паспортном щитке трансформатора указывается его номинальное напряжение - высшее и низшее, в соответствии с чем следует различать обмотку высшего напряжения (ВН) и обмотку низшего напряжения (НН) трансформатора. Кроме того, на щитке указывается полная номинальная мощность (В×А или кВ×А), токи (А) при полной номинальной мощности, частота, число фаз, схема соединения, режим работы (длительный или кратковременный) и способ охлаждения (воздушный или масляный).

Если первичное напряжение U₁ трансформатора меньше вторичного U₂, то он работает как повышающий трансформатор; в противном случае (U₁> U₂) – как понижающий.

Одним из основных параметров трансформаторов является коэффици-ент полезного действия (КПД) – η. Его оценивают отношением активной мощности, передаваемой в нагрузку – Р₂, к активной мощности, поступающей в первичную обмотку трансформатора – Р₁, т. е.

η = Р₂/Р₁.

Как и любое техническое устройство, трансформатор имеет потери энергии. Это потери в стали – Р_С и потери в проводах – Р_ПР первичной и вторичной обмоток трансформатора. Распределение потерь наглядно демонстрирует энергетическая диаграмма рис. 10.3.

Следует подчеркнуть, что диаграмма иллюстрирует только качественную картину распределения потерь активной мощности на элементах конструкции трансформатора. Количественно потери составляют единицы процентов от общей мощности. Трансформаторы обладают очень высоким КПД, значение которого, для мощных силовых трансформаторов достигает 99%.

Трансформаторы играют важную роль в электроэнергетических системах. Они осуществляют многоступенчатую трансформацию напряжений, обеспечивая экономичную передачу электроэнергии. Число ступеней трансформации практически совпадает с сеткой номинальных напряжений: 0,22; 0,38; 0,66; 1,0; 3,0; 6,0; 10; 20; 35; 110; 150; 220; 350; 500; 750; 1050 кВ.

Трансформаторы, используемые в системах распределения электроэнергии, называются силовыми. Они имеют полную номинальную мощность

от 10 кВ∙А до 1 млн. кВ∙А.

В сварочных трансформаторах используется возможность снизить

напряжение до безопасного уровня и обеспечить гальваническую развязку рабочего места с цепью высокого напряжения.

В устройствах промышленной электроники применяют высокочастотные и импульсные трансформаторы, мощность которых изменяется в пределах от нескольких милливатт до 1000 В∙А.

Свойства трансформаторов используется в измерительной технике. Они позволяют измерять параметры цепей высокого напряжения на стороне вторичной обмотки, имеющей низкое напряжение и хорошее заземление.

2. ПРИНЦИП РАБОТЫ ОДНОФАЗНЫХ ТРАНСФОРМАТОРОВ

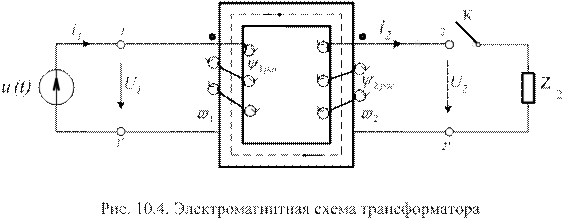
Принцип работы однофазных трансформаторов рассмотрим по схеме рис.10.4. При подключении источника напряжения 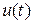в первичной обмотке трансформатора возникает ток 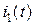. Далее будем пользоваться действующими значениями используемых физических величин.

Ток 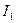приводит к появлению магнитодвижущей силы первичной обмотки

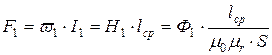. (10.1)

Магнитодвижущая сила 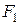возбуждает в магнитопроводе магнитный поток 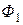, причем

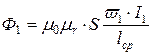. (10.2)

Магнитный поток 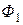индуцирует в первичной обмотке трансформатора Э.Д.С. самоиндукции 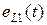, а во вторичной обмотке – Э.Д.С. взаимной индукции .

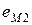Замкнем цепь вторичной обмотки. Под воздействием ЭДС взаимной индукции через нагрузку Z₂ потечет ток I₂ , возникает магнитодвижущая

сила F₂, и магнитный поток Ф₂, причем

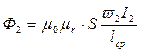. (10.3)

Для указанных на рис.10.2 направлений намотки обмоток трансформатора и выбранных положительных направлений токов I₁ и I₂ магнитные потоки Ф₁ и Ф₂ встречные. Поэтому в магнитопроводе создается результирующий магнитный поток

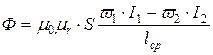. (10.4)

Этот поток пересекает витки обеих обмоток трансформатора и наводит в них результирующие Э.Д.С. е₁ и е_{2 .}

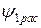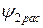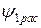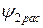Помимо основного магнитного потока Ф (по 10.4) в реальном трансформаторе существуют потоки рассеяния первичной и вторичной обмоток. Для количественной оценки потоков и вводят понятие эквивалентной индуктивности рассеяния так, что

; .

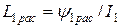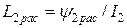Кроме того, обмотки реального трансформатора обладают активными

сопротивлениями R₁ и R₂. Чтобы учесть перечисленные величины при анализе работы трансформатора, переходят к его схеме замещения (рис.10.5).

.

Часть схемы, выделенная на рис. 10.5 пунктиром, не имеет активных сопротивлений и потоков рассеяния, а поэтому называется идеализированным трансформатором. К нему применимы все соотношения, полученные в лекции №8. Однако для получения простых и наглядных соотношений параметров трансформатора необходимо преодолеть еще одну трудность.

Дело в том, что трансформатор в расчетном эквиваленте представляет собой нелинейную цепь. Значит, к его анализу необходимо применять теорию нелинейной алгебры. Чтобы уйти от этого, гистерезисную зависимость В = f(H) заменяют эквивалентным эллипсом (рис.10.6), построенным так, что его площадь не менее чем на 95% перекрывает площадь петли гистерезиса.

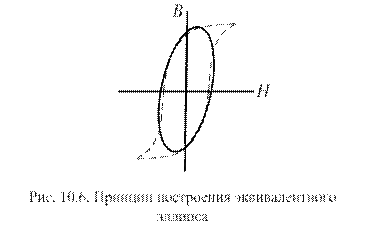
Если теперь зависимости B = f(H), 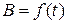; 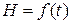выражать через

параметры эллипса, то возникающие за счет отклонения от петли гистерезиса погрешности оказываются пренебрежимо малыми для практических целей. Главное в том, что переход к параметрам эквивалентного эллипса позволяет получить простые линейные выражения в представлении величин В(t) и Н(t) с помощью тригонометрических функций:

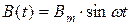, (10.5)

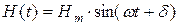, (10.6)

где 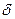- сдвиг фазы между Н(t) и В(t).

От выражений (10.5) и (10.6) легко перейти к показательной комплексной форме представления. Тогда

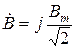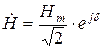; , (10.7)

Учитывая соотношения (8.3), (8.15) и (10.7), связь между напряжением и магнитной индукцией представим в виде:

,

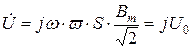а связь между током и напряженностью магнитного поля выражением:

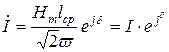. (10.8)

Теперь можно перейти к оценке основных параметров трансформатора. Учитывая (8.3), (8.15) и (10.7), определяем напряжение на первичной и вторичной обмотках трансформатора:

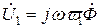, (10.9)

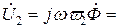
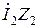. (10.10)

Эти напряжения полностью уравновешиваются Э.Д.С. первичной 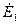и вторичной 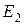обмоток:

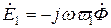, (10.11)

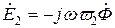. (10.12)

Отношение (10.10) к (10.9):

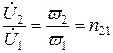(10.13)

называется коэффициентом трансформации.

Подставим в выражение для 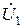значение Ф из (10.4):

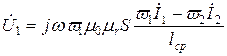. (10.14)

Если разомкнуть цепь вторичной обмотки, то ее ток I₂ станет равным

нулю. При этом в цепи первичной обмотки будет протекать ток холостого хода, т.е. I₁ = I_1x , а выражение (10.14) примет вид:

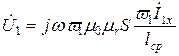. (10.15)

Но 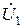- это напряжение источника. Оно не зависит от режима работы трансформатора. Значит, левые части равенств (10.14) и (10.15) равны.

Отсюда следует, что равны и правые части. Приравнивая их, определим ток

холостого хода трансформатора.

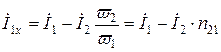. (10.16)

Последнее выражение показывает, что ток холостого хода равен разности токов первичной и вторичной обмоток, причем ток вторичной обмотки пересчитан к виткам первичной обмотки. Ток холостого хода мал и у мощных трансформаторов составляет единицы процентов от номинального значения.

Произведение

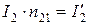
называют приведенным током вторичной обмотки. Для оценки качества трансформатора кроме 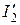пользуются приведенным сопротивлением нагрузки 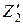и приведенным напряжением вторичной обмотки 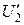. Определим их значения. Для этого выразим магнитный поток Ф из (10.10)

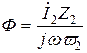. (10.17)

Подставим (10.17) в (10.9):

.

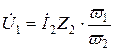Помножим и разделим последнее выражение на коэффициент 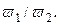Перегруппировав множители, получим:

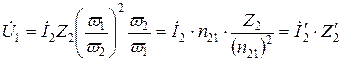. (10.18)

В выражении (10.18) 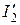- приведенный ток, а 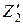- приведенное, т.е. пересчитанное к виткам первичной обмотки, сопротивление нагрузки. Произведение

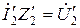(10.19)

называется приведенным напряжением вторичной обмотки. Очевидно, что

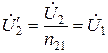. (10.20)

С учетом введенных понятий выражение (10.16) для тока холостого хода принимает вид:

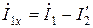. (10.21)

В выражении (10.15) множитель

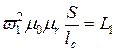
определяет индуктивность первичной обмотки. Поэтому можно записать:

,

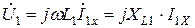что полностью соответствует закону Ома для цепи с индуктивностью.

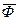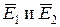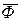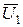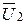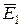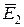Для завершения анализа принципа работы построим векторную диаграмму идеализированного трансформатора (рис.10.7). На диаграмме в качестве исходного принимаем вектор магнитного потока . Векторы Э.Д.С. отстают от вектора на 90⁰. Это очевидно из (10.11) и (10.12) по наличию множителя (-j). Векторы и равны по величине векторам и соответственно, но противоположны им по направлению.

Вектор тока холостого хода 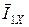опережает вектор 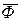на угол d. Это

хорошо видно из (10.8), т.к.

.

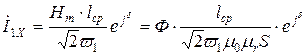Вектор тока вторичной обмотки трансформатора 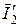сдвинут относительно вектора 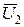на угол j₂, что определяется характером нагрузки

.

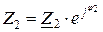Значение вектора 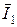легко найти по (10.21).

,

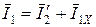что и выполнено на диаграмме.

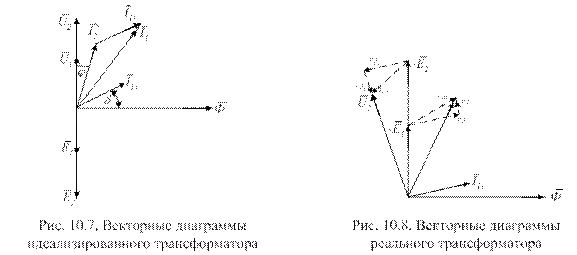
Для перехода к реальному трансформатору обратимся к рис. 10.5. Схема рис. 10.5 содержит два электрически не связанных замкнутых контура – цепь первичной и цепь вторичной обмоток. Для каждой из них справедлив второй закон Кирхгофа. Поэтому для цепи первичной обмотки трансформатора справедливо равенство

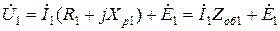. (10.22)

Равенство (10.22) показывает, что напряжение источника 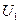уравновешивается падением напряжения на комплексном сопротивлении первичной обмотки и наводящейся в ней ЭДС самоиндукции 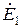. Эпюры напряжений, соответствующие (10.22), приведены на рис. 10.8.

Для цепи вторичной обмотки трансформатора можно записать равенство

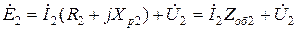. (10.23)

Эпюры напряжения, соответствующие (10.23), приведены на рис. 10.8.

3. РЕЖИМЫ РАБОТЫ ТРАНСФОРМАТОРОВ

Различают несколько режимов работы трансформаторов:

1. Номинальный режим, т.е. режим при номинальных значениях напряжения и тока первичной обработки трансформатора:

.

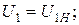
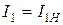2. Рабочий режим, при котором напряжение первичной обмотки близко к номинальному или равно ему, а ток 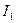определяется нагрузкой трансформатора.

3. Режим холостого хода, т.е. режим ненагруженного трансформатора, при котором цепь вторичной обмотки разомкнута ( 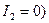или подключена к нагрузке с очень большим сопротивлением (например, в цепь включен вольтметр).

4. Режим короткого замыкания трансформатора, при котором его вторичная обмотка замкнута накоротко ( 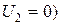или подключена к нагрузке с очень малым сопротивлением (например, в цепь включен амперметр).

Обычно трансформаторы эксплуатируются в рабочем режиме. Номинальный режим работы возникает, когда нагрузка соответствует номинальной. Режимы холостого хода и короткого замыкания в обычных условиях не допускаются. Они возникают при авариях. Но режимы холостого хода и короткого замыкания могут создаваться специально, для испытания трансформаторов на заводах изготовителях или в специальных лабораториях. Такие испытания проводят для экспериментального определения параметров вновь созданных трансформаторов и называются опытами холостого хода и короткого замыкания. Рассмотрим их более внимательно.

3.1.Опыт холостого хода трансформатора

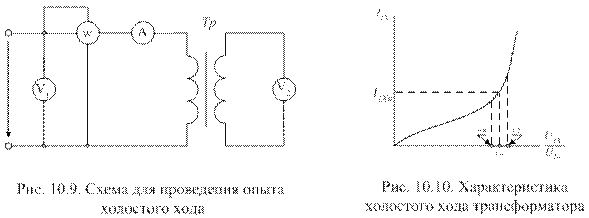
Опытом холостого хода называют испытание трансформатора при

разомкнутой цепи вторичной обмотки и номинальном напряжении на первичной обмотке. Схема для проведения опыта холостого хода приведена на рис.10.9. Полагая, что измерительные приборы не вносят в режим работы трансформатора сколько-нибудь ощутимых изменений, можем измерить ряд его параметров(U_1Н, I_1Х, U_2Н, Р_С), а затем дополнить это ряд расчетами(I_1Н, n₂₁).

Опыт холостого хода начинают проводить с установки номинального напряжения на первичной обмотке трансформатора. Величину напряжения контролируют по показаниям вольтметра V₁. Показания амперметра, при 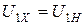, определяют номинальное значение тока холостого хода - 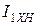. Учитывая, что этот ток составляет 3 ¸ 10% от номинального тока первичной обмотки для мощных трансформаторов и до 40% для маломощных, можем рассчитать значение номинального тока первичной обмотки

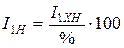. (10.24)

Кроме этого, при разомкнутой цепи вторичной обмотки всегда 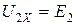. Это значит, что

.

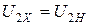Измерив вольтметрам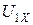и и 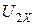, легко определить коэффициент трансформации

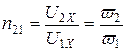. (10.25)

Мощность потерь в трансформаторе при холостом ходе складывается из мощности потерь в магнитопроводе – Р_с и в проводах – Р_пр. Мощность потерь в магнитопроводе пропорциональна квадрату магнитной индукции - В², а, значит, и квадрату напряжения первичной обмотки – 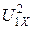. Так как 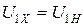, то и потери в магнитопроводе соответствуют номинальному значению.

Потери в проводах вторичной обмотки отсутствуют, так как 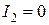. Потери в проводах первичной обмотки пропорциональны квадрату тока холостого хода ( 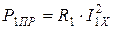). Но ток холостого хода пренебрежимо мал в сравнении с номинальным током. Поэтому и мощность потерь в проводах ничтожна по сравнению с мощностью потерь в магнитопроводе. Отсюда следует, что показания ваттметра в опыте холостого хода определяют только потери в магнитопроводе – Р_с.

Следует учитывать, что потери Р_с складываются из потерь на гистерезис и дополнительных потерь на вихревые токи, потерь в деталях конструкции и потерь из-за вибрации листов стали магнитопровода. Однако эти дополнительные потери не превышают 20% от общих потерь.

В ряде случаев важно знать, как изменится ток холостого хода трансформатора при изменении напряжения на первичной обмотке. Зависимость 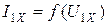приведена на рис. 10.10. Она называется характеристикой холостого хода трансформатора.

При малых значениях 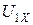значение магнитной индукции 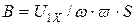мало. Магнитопровод не насыщен, поэтому 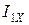увеличивается пропорционально напряжению. При увеличении 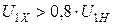начинает сказываться насыщение магнитопровода и приращение тока холостого хода увеличивается.

Магнитопровод трансформатора проектируют так, чтобы значение магнитной индукции не превышало величины 1,6¸ 1,7 Тл. При таком значении магнитной индукции увеличение 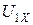до 1,2 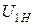не приводит к критическому увеличению тока холостого хода и допустимо в течение длительного времени.

3.2. Опыт короткого замыкания трансформатора

Опытом короткого замыкания называется испытание трансформатора при короткозамкнутой цепи вторичной обмотки и номинальном токе первичной обмотки. Схема для проведения опыта короткого замыкания приведена на рис. 10.11. Опыт проводится для определения номинального значения тока вторичной обмотки, мощности потерь в проводах и падения напряжения на внутреннем сопротивлении трансформатора.

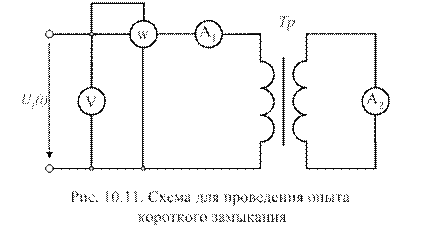
При коротком замыкании цепи вторичной обмотки ток в ней ограничивается только малым внутренним сопротивлением этой обмотки. Поэтому даже при относительно небольших значениях ЭДС Е₂ ток I₂ может достигнуть опасных величин, вызвать перегрев обмоток, разрушение изоляции и выход трансформатора из строя.

Учитывая это, опыт начинают при нулевом напряжении на входе

трансформатора, т.е. 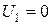. Постепенно увеличивая напряжение первичной обмотки наблюдают за значением тока I₁.Когда величина тока I₁ достигнет значения I_1Н, напряжение U₁ фиксируют. Эту величину называют напряжением короткого замыкания и обозначают U_1К. Величину тока вторичной обмотки, измеренную амперметром А₂ при U₁ = U_1К, принимают номинальной.

Величина напряжения первичной обмотки в опыте короткого замыкания 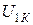мала и составляет (5 ¸ 10)% от номинального. Поэтому и действующее значение Э.Д.С. вторичной обмотки Е₂ составляет (2 ¸ 5)%. Так как магнитный поток пропорционален значению Э.Д.С., то и мощность потерь в магнитопроводе – Р_с пренебрежимо мала. Отсюда следует, что показания ваттметра в опыте короткого замыкания практически определяют только потери в проводах Р_пр.

Определим падение напряжения на внутреннем сопротивлении трансформатора. Очевидно, что комплексное внутреннее сопротивление трансформатора имеет индуктивный характер. Чтобы оценить его составляющие, проведем ряд преобразований. Учтем, что

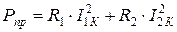. (10.26)

Выразим ток I_2К через приведенный ток I'₂:

.

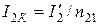Учтем, что 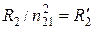, а также, что 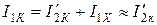. Тогда выражение (10.26) можно переписать в виде:

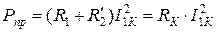, (10.27)

где R_К - активное сопротивление трансформатора в режиме короткого замыкания, причем:

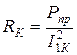. (10.28)

Знание активного сопротивления трансформатора позволяет рассчитать его индуктивное сопротивление:

.

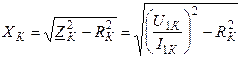При точном расчете нужно учитывать, что R_К зависит от температуры. Поэтому полное сопротивление трансформатора определяют приведенным к температуре 75⁰С, т.е.

.

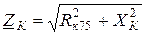Теперь легко определить падение напряжения на внутреннем сопротивлении трансформатора :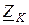

.

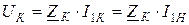На практике пользуются приведенным значением U_К, в процентах, обозначая его звездочкой, т.е.

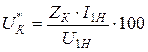. (10.29)

Это значение приводят на паспортном щитке трансформатора.

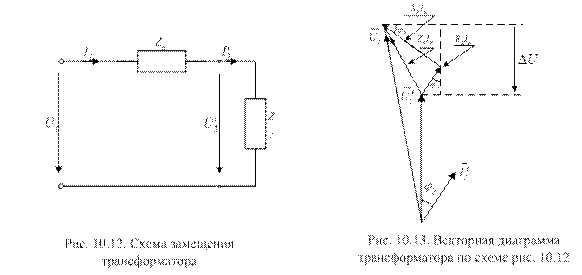
В ряде практических случаев необходимо знать величину уменьшения напряжения на выходе трансформатора ∆U за счет падения напряжения на его внутреннем сопротивлении. Чтобы определить эту величину, составим новую схему замещения трансформатора, содержащую Z_К. Знание внутреннего сопротивления трансформатора позволяет представить его схему замещения в виде рис.10.12. Векторная диаграмма, соответствующая этой схеме, приведена на рис. 10.13.

Векторная диаграмма позволяет определить уменьшение напряжения на выходе трансформатора DU за счет падения напряжения на его комплексном сопротивлении. Величина DU определяется как расстояние между прямыми, выходящими из точек начала и конца вектора 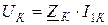и параллельными оси абсцисс. Из диаграммы видно, что эта величина складывается из катетов двух прямоугольных треугольников, гипотенузы которых 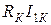и 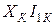, а острые углы равны j₂.Поэтому

.

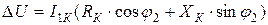На практике пользуются относительной величиной DU, в процентах, обозначенной звездочкой, т.е.

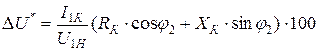. (10.30)

Для мощных трансформаторов (при S_H > 1000 В×А) опыт короткого замыкания может служить для контроля коэффициента трансформации. Для таких трансформаторов в режиме короткого замыкания током холостого хода можно пренебречь, считая

.

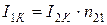Поэтому

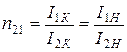. (10.31)

Последнее выражение тем точнее, чем больше мощность трансформатора. Однако оно не приемлемо для маломощных трансформаторов.

4. ВНЕШНЯЯ ХАРАКТЕРИСТИКА ТРАНСФОРМАТОРА

Внешняя характеристика трансформатора определяет зависимость напряжения вторичной обмотки U₂ от тока вторичной обмотки I₂ при постоянном коэффициенте мощности cosj₂ = const и номинальном напряжении первичной обмотки U₁. Часто для определения внешней характеристики пользуются относительными единицами (рис.10.14).

,

,

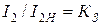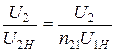где 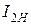– ток нагрузки при номинальном токе первичной обмотки, 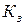– коэффициент загрузки трансформатора.

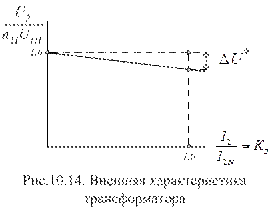
Так как 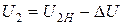, U_2Н = n₂₁∙U₁, a ∆U = ∆U*∙U_2Н/100, то достаточно просто получить равенство, определяющее значение ординаты внешней характеристики трансформатора:

,

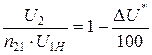где 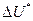определяется по (10.30).

Раскроем правую часть последнего равенства:

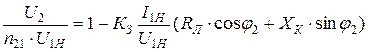. (10.32)

Выражение (10.32) показывает, что напряжение на выходе трансформатора зависит от параметров его внутреннего сопротивления (R_К, X_к), коэффициента мощности cosj₂ и коэффициента загрузки. График представляет наклонную линию. Трансформаторы проектируют так, чтобы при номинальном токе вторичной обмотки снижение выходного пряжения не превышало (5 ¸ 10)% от номинального.

5. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ

ТРАНСФОРМАТОРА

Коэффициент полезного действия (КПД) трансформатора определя-ется отношением активной мощности Р₂ на выходе трансформатора к активной мощности Р₁ на его входе

.

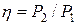Мощные современные трансформаторы могут иметь КПД больше 99%. В таких случаях мощности Р₂ и Р₁ настолько близки, что не существует измерительных приборов, способных их отличить. Поэтому КПД определяют косвенным методом, основанном на прямом измерении мощности Р₂ и мощности потерь DР.

Так как

,

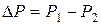то

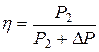. (10.33)

Мощность потерь в трансформаторе ∆Р равна сумме мощностей потерь в магнитопроводе - Р_С и в проводах Р_пр. Потери в магнитопроводе пропорциональны напряжению первичной обмотки U₁. Обычно трансформаторы работают при номинальном напряжении первичной обмотки. Поэтому считают Р_С= const. Их определяют в опыте холостого хода.

Потери в проводах обмоток определяются токами обмоток, которые, в свою очередь, зависят от характера нагрузки. Так как нагрузка силовых трансформаторов часто изменяется, то и потери в проводах переменные. Найдем выражение, удобное для их учета. Для этого вспомним, что ток холостого хода трансформатора пренебрежимо мал в сравнении с номинальным.

Поэтому будем полагать, что в рабочем режиме

.

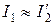Воспользовавшись понятием коэффициента загрузки трансформатора,

можем записать:

.

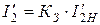Теперь выражение (10.27) можно записать в виде:

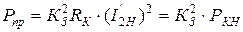, (10.34)

где 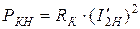– мощность потерь в проводах обмоток при номинальных токах.

Величина Р_КН постоянная и определяется в опыте короткого замыкания.

Мощность на выходе трансформатора определяется известным выражением

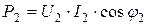. (10.35)

Так как 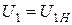, то и 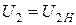. Тогда, применяя коэффициент загрузки трансформатора, перепишем (10.35) в виде:

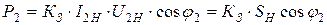, (10.36)

где S_H - полная номинальная мощность трансформатора.

Подставляя (10.34) и (10.36) в (10.33) получаем окончательное выражение для КПД:

.

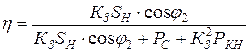Выражение показывает, что КПД трансформатора зависит от значений коэффициента мощности нагрузки – cos j₂ и от коэффициента загрузки – К_З. На практике максимум КПД достигается при средней нагрузке, когда К_З = 0,7 ¸ 0,5, а отношение Р_С / Р_КН = 0,5 ÷ 0,25.

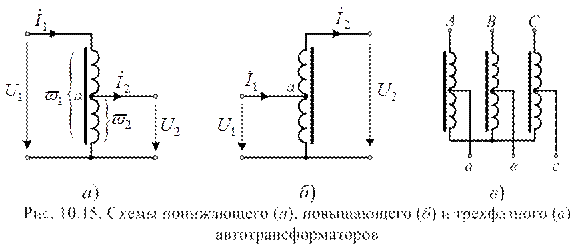
6. АВТОТРАНСФОРМАТОРЫ

Среди силовых трансформаторов особое место занимают автотрансформаторы. Их применение становится целесообразным при значениях коэффициента трансформации не более 2. В этом случае КПД автотрансформатора выше, а размеры меньше, чем у обычных силовых трансформаторов.

Автотрансформатор отличается от трансформатора тем, что имеет лишь обмотку высшего напряжения. Обмотка низшего напряжения является частью обмотки высшего напряжения. Обмотка высшего напряжения автотрансформатора может быть первичной (рис. 10.15, а) или вторичной (рис. 10.15, б).

При заданном первичном напряжении автотрансформатора по схеме рис. 10.15, а, при известном числе витков 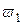амплитуду магнитного потока Ф_м в магнитопроводе можно определить по (10.9), т. е. 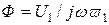. Этот магнитный поток индуцирует в каждом витке обмотки Э.Д.С., практически не зависящую от тока в обмотке. Следовательно, напряжения между отдельными частями обмотки поддерживаются постоянными. Напряжения и токи автотрансформатора связаны теми же соотношениями, что и в трансформаторе:

.

Фазы токов в обмотках трансформатора одинаковы. Поэтому, пренебрегая влиянием намагничивающего потока, можно считать, что в общей части обмотки действующее значение тока равно разности токов I₁ – I₂.

Если коэффициент трансформации 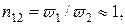то действующие значения токов I₁ и I₂ почти одинаковы, а их разность мала по сравнению с каждым из них. Поэтому общую часть первичной и вторичной обмоток можно сделать из более тонкого провода, т. е. стоимость и размеры автотрансформатора меньше, чем трансформатора.

У трехфазных автотрансформаторов обмотки обычно соединяются по схеме “звезда” c выведенной нейтральной точкой или без нее (рис. 10.15, в).

В настоящее время мощные автотрансформаторы применяют на подстанциях с номинальными напряжениями 110 и 220 кВ, 154 и 220 кВ и т. п. Автотрансформаторы применяют для понижения напряжения на зажимах мощных синхронных и асинхронных двигателей при их пуске. В электротермии их часто используют для ступенчатого регулирования напряжения на нагревательных элементах печей.

В лабораториях широкое применение находят автотрансформаторы низкого напряжения с плавной регулировкой выходного напряжения (ЛАТР).

6.1. Индукционные катушки.

Автотрансформаторная связь широко используется в слаботочных цепях для создания устройств различного назначения. Одно из таких устройств – индукционные катушки или катушки зажигания. Они широко применяются в системах зажигания двигателей внутреннего сгорания. Рассмотрим принцип применения катушек зажигания более подробно.

Упрощенная схема системы зажигания двигателя с одним цилиндром приведена на рис. 10.16, а. Принцип ее работы легко применить к любому числу цилиндров.

Схема включает аккумуляторную батарею Е, катушку зажигания с первичной 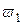и вторичной 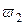обмотками, прерыватель К₂, конденсатор первичной цепи С₁, добавочный резистор R, выключатель К₁ и свечу зажигания. Частота, с которой замыкаются контакты прерывателя К₂, определяется частотой вращения вала двигателя – n(об/мин). Выключатель К₁ замыкается во время пуска двигателя.

При замыкании контактов прерывателя К₂ через первичную обмотку катушки протекает ток, нарастая от нуля до некоторого значения. Его величину можно определить выражением:

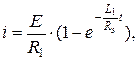
где L₁ – индуктивность первичной обмотки, R_э – эквивалентное сопротивление цепи первичной обмотки (сумма сопротивлений первичной обмотки, добавочного резистора R и проводов).

Время t, в течение которого нарастает ток i, зависит от частоты вращения вала двигателя n, числа цилиндров z, конструкции прерывателя. Постоянная цепи τ₁ = L₁/R_э подбирается так, чтобы ток достигал максимального значения за время ≈ 0,2 с. Обозначим ток к концу интервала нарастания i_р. <