Взаимная индуктивность, согласное и встречное включение катушек
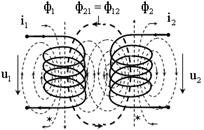
Рассмотрим электрическую цепь, состоящую из двух катушек индуктивности (рис. 7.1, а). Пусть по проводникам первой катушки индуктивности протекает переменный ток 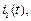 тогда на ее зажимах наводится ЭДС самоиндукции, которая обусловлена собственным магнитным потоком Ф1(t):
тогда на ее зажимах наводится ЭДС самоиндукции, которая обусловлена собственным магнитным потоком Ф1(t):
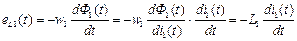 .
.
 а а
|  б б
|
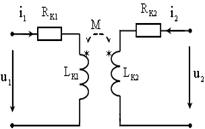
| Рис. 7.1. Электрические цепи с магнитными связями |
Если часть этого потока 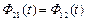 пересекает контур, образованный витками другой катушки индуктивности, то в последней находится ЭДС взаимоиндукции:
пересекает контур, образованный витками другой катушки индуктивности, то в последней находится ЭДС взаимоиндукции:
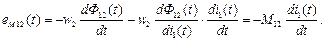
Аналогично находится ЭДС во второй катушке. В общем случае можно определить напряжение на зажимах каждой катушки:
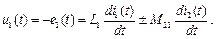
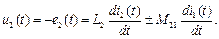 (7.1)
(7.1)
В линейной магнитной среде коэффициенты 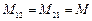 и называются взаимной индуктивностью.
и называются взаимной индуктивностью.
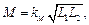
где 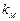 – коэффициент магнитной связи (
– коэффициент магнитной связи ( 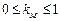 ).
).
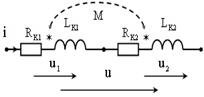
Выбор знака в (7.1) зависит от ориентации токов относительно так называемых одноименных зажимов. Одноименные зажимы – это зажимы, выбранные таким образом, что при одинаковом направлении токов относительно этих зажимов, магнитные потоки самоиндукции и взаимоиндукции суммируются. Одноименные зажимы помечают одинаковыми символами, например звездочками. Если магнитные потоки обеих катушек складываются (рис. 7.1, а), то токи i1(t) и i2(t) одновременно должны входить или выходить из зажимов, помеченных звездочками (рис. 7.1, б), а если магнитные потоки обеих катушек вычитаются, то один ток должен входить, а второй выходить из помеченного звездочкой зажима (рис. 7.2).
 а
а
|  б
б
|
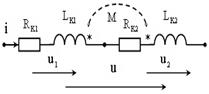
| Рис. 7.2. Согласное и встречное соединение |
Включение катушек по схеме рис. 7.2, а называется согласным, а по схеме рис. 7.2, б – встречным. В уравнениях (7.1) для согласного включения берется знак «плюс», а для встречного – знак «минус».
Если напряжение u(t) меняется по гармоническому закону, то, применяя символический метод, получим комплексное действующее значение общего напряжения при согласном включении:
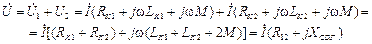
и при встречном включении:
|
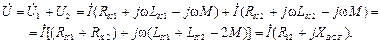
Если значения 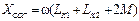 и
и 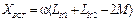 измерены, то
измерены, то
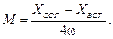 (7.2)
(7.2)
Выражение (7.2) может использоваться для экспериментального определения взаимной индуктивности.
Дата добавления: 2020-10-14; просмотров: 1233;











