Основы фильтрации в частотной области

<2 3 456 7 8 >

Каждый элемент фурье-образа 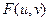содержит все отсчеты функции 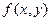. Поэтому обычно, за исключением тривиальных случаев, невозможно установить прямое соответствие между характерными деталями изображения и его фурье-образа. Однако некоторые общие утверждения относительно взаимосвязи частотных составляющих фурье-образа и пространственных характеристик изображения могут быть сделаны. Частоты в фурье-преобразовании связаны с вариацией яркости на изображении. Наиболее медленно меняющаяся (постоянная) частотная составляющая (u=v=0) совпадает со средней яркостью изображения. Низкие частоты, отвечающие точкам вблизи начала координат фурье-преобразования, соответствуют медленно меняющимся компонентам изображения. На изображении комнаты, например, они могут соответствовать плавным изменениям яркости стен и пола. По мере удаления от начала координат, более высокие частоты начинают соответствовать все более и более быстрым изменениям яркости, которые суть границы объектов (контуры) и другие детали изображения, характеризуемые резкими изменениями яркости, такие как шум.

Один из часто используемых способов обработки изображения, которая выполняется с различными целями, является частотная фильтрация.

Процедура фильтрации в частотной области состоит из следующих шагов (рис.1.7):

1. Исходное изображение умножается на 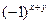, чтобы его преобразование Фурье оказалось центрированным.

2. Вычисляется прямое ДПФ 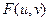изображения, полученного после шага 1.

3. Функция 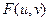умножается на функцию фильтра .

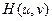4. Вычисляется обратное ДПФ от результата шага 3.

5. Выделяется вещественная часть результата шага 4.

6. Результат шага 5 умножается на .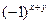

Пусть 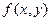обозначает входное изображение после шага 1, 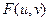- его фурье-образ. Тогда фурье-образ выходного изображения определяется выражением:

.

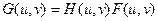Умножение функций двух переменных 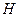и осуществляется поэлементно, т.е. первый элемент функции 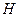умножается на первый элемент функции , второй элемент функции 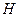умножается на второй элемент функции и т.д. В общем случае компоненты фильтра 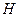являются комплексными величинами. На практике чаще всего используются 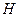с действительными компонентами. В этом случае и действительная и мнимая части функции умножаются на одну и ту же действительную функцию фильтра 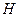. Такие фильтры называются фильтрами нулевого фазового сдвига, поскольку не меняют фазу фурье-преобразования.

Фильтрованное изображение получается вычислением обратного преобразования Фурье от фурье-образа :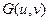

Фильтрованное изображение = F^-1 .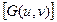

Искомое изображение получается выделением действительной части из последнего результата и умножения на 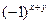, чтобы скомпенсировать эффект от умножения входного изображения на ту же величину. Обратное фурье-преобразование в общем случае является комплексным. Однако в случае вещественного входного изображения и вещественной функции фильтра мнимые части всех значений обратного фурье-преобразования должны равняться 0. Но на практике значения обратного фурье-преобразования, как правило, содержат паразитную мнимую составляющую, что связано с ошибками округлений при вычислениях. Этой составляющей необходимо пренебречь.

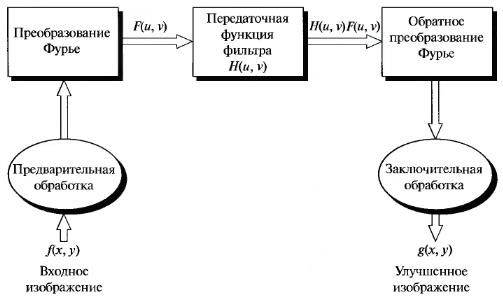
Рис.1.7. Основные этапы фильтрации в частотной области

Модели шума

Как и при улучшении ЦИ, конечной целью восстановления является повышение качества изображения в некотором заранее предопределенном смысле. Улучшение ЦИ является в большей степени субъективной процедурой, а процесс восстановления, в основном, имеет объективный характер. При восстановлении делается попытка реконструировать или воссоздать изображение, которое было до этого искажено, используя априорную информацию о явлении, которое вызвало ухудшение изображения. Поэтому методы восстановления основаны на моделировании процессов искажения и применении обратных процедур для воссоздания исходного изображения.

Этот подход обычно включает в себя разработку критериев качества, которые дают возможность объективно оценить полученный результат. Напротив, методы улучшения изображения в основном представляют собой эвристические процедуры, предназначенные для такого воздействия на изображение, которое позволит затем использовать преимущества, связанные с психофизическими особенностями зрительной системы человека.

Как показано на рис.1.8, модель процесса искажения предполагает действие некоторого искажающего оператора 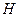на исходное изображени 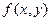, что после добавления аддитивного шума дает искаженное изображение 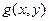. Задача восстановления состоит в построении некоторого приближения 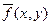исходного изображения по заданному (искаженному) изображению 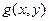, некоторой информации относительно искажающего оператора 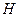, и некоторой информации относительно аддитивного шума 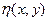. Желательно, чтобы приближение было как можно ближе к исходному изображению.

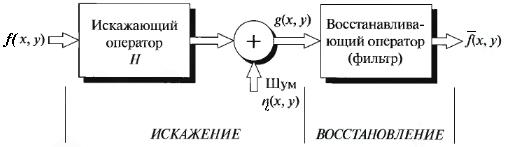
Рис.1.8. Модель процесса искажения/восстановления изображения

Для простоты далее полагаем, что 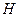- тождественный оператор, и мы имеем дело только с искажениями, вызванными наличием шума.

Основные источники шума на цифровом изображении:

· Процесс получения (оцифровки) ЦИ (работа сенсоров зависит от различных факторов, таких как внешние условия (например, уровень освещенности) в процессе видеосъемки и качество сенсоров (например, их температура));

· Процесс передачи ЦИ (изображения в процессе передачи могут искажаться помехами, возникающими в канале связи. Например, при передаче изображения с использованием беспроводной связи оно может быть искажено в результате разряда молнии или других возмущений в атмосфере).

Подробно модели шума рассмотрены в соответствующем разделе МУ.Стего.

<2 3 456 7 8 >

Дата добавления: 2016-07-22; просмотров: 4474;