Возможные способы сжатия ЦИ

ПРИМЕР 1. Сжатие посредством квантования. Рассмотрим ЦИ на рис.2.1(а) – 256 градаций яркости (8 бит). Рис. 2.1(б) – то же ЦИ после равномерного квантования на 16 уровней (4 бита). Полученный в результате коэффициент сжатия равен 2:1. На гладких областях (рис.2.1(б)) появились ложные контура. Улучшение на рис.2.1(в). Здесь производилось квантование, основанное на особенностях зрительной системы человека. Коэффициент сжатия здесь также 2:1, но ложных контуров практически нет, но появилась дополнительная зернистость.

Рис.2.1. Исходное изображение (а); равномерное квантование на 16 уровней (б); модифицированное квантование яркости на 16 уровней (в)

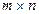ПРИМЕР 2. Сжатие посредством использования малоранговых аппроксимаций изображения. Пусть — матрица ЦИ размерами с элементами 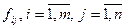, ( 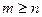). Для нее справедливо представление, называемое сингулярным разложением (SVD):

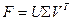, (2.1)

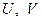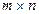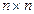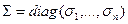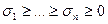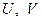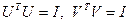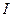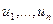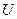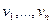где ― матрицы размерности и соответственно; , . При этом удовлетворяют соотношениям: , где ― единичная матрица соответствующего размера, т.е. являются ортогональными. Столбцы матрицы и матрицы 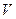называют соответственно левыми и правыми сингулярными векторами матрицы , величины 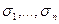― сингулярными числами (СНЧ), а 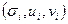назовем сингулярной тройкой . (При 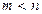рассматривается SVD матрицы .)

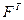Сингулярное разложение (2.1) матрицы может быть представлено в форме внешних произведений:

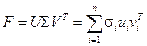(2.2)

В общем случае SVD матрицы определяется неоднозначно. Назовем вектор 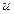лексикографически положительным, если его первая ненулевая компонента положительна, а SVD (2.1) нормальным, если столбцы матрицы 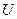лексикографически положительны. Можно показать, что невырожденная матрица имеет единственное нормальное SVD, если ее СНЧ попарно различны. Таким образом, СНЧ и сингулярные векторы (СНВ), получаемые нормальным SVD, однозначно определяют матрицу ЦИ.

Пусть 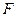― симметричная 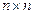-матрица, элементы которой 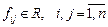, с собственными значениями (СЗ) 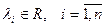, и ортонормированными собственными векторами (СВ) 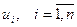, спектральное разложение (СР) которой определяется в соответствии с формулой:

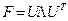(2.3)

где 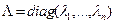― матрица СЗ; 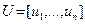― матрица СВ.

Разложение (2.3), так же, как и (2.1), может быть представлено в форме внешних произведений:

.

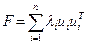В силу симметричности 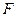ее спектр, т.е. множество всех СЗ, всегда действительный. СЗ, являясь корнями характеристического многочлена 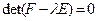, определяются однозначно, в отличие от СР (2.3).

По аналогии с нормальным SVD, СР назовем нормальным, если элементы матрицы 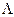удовлетворяют соотношению: 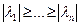, а СВ , лексикографически положительны. Имеет место следующая теорема.

Теорема. Пусть 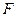— невырожденная симметричная 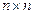-матрица, модули СЗ которой попарно различны. Тогда для нее существует единственное нормальное СР.

Как правило, матрица ЦИ не удовлетворяет свойству: 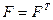. Поставим в соответствие произвольной две симметричные матрицы 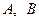той же размерности по следующему правилу:

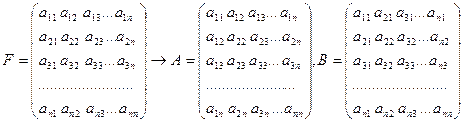. (2.4)

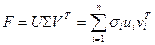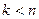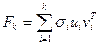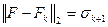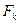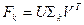Утверждение. Для матрицы ближайшей в смысле спектральной нормы матрицей ранга является матрица , причем . Для матрицы , называемой малоранговой аппроксимацией , справедливо также представление , где .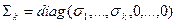

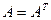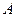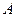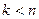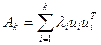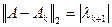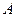Утверждение. Пусть . Для матрицы построено нормальное СР (2.3). Ближайшей к в смысле спектральной нормы матрицей ранга является , причем . Для матрицы , называемой малоранговой аппроксимацией , справедливо также представлени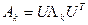е , где .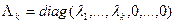

Малоранговые аппроксимации матрицы ЦИ могут быть использованы для сжатия изображения. Пусть матрица имеет размеры 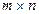, тогда нужно хранить 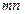ее элементов. С учетом того, что матрицы оригинальных ЦИ, как правило, имеют значительные размеры, актуальным является вопрос о том, можно ли сократить это количество? Рассмотрим в качестве примера ЦИ на рис.2.2(а), размеры которого 480*640. Построим SVD матрицы ЦИ. Матрица 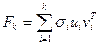есть наилучшее приближение ранга 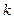, при этом для восстановления матрицы 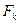требуется лишь 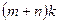слов памяти, в которых хранятся векторы 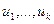и 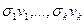. Приближения исходного ЦИ для различных значений 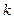показаны на рис.2.2(б,в,г)

а б

в г

Рис.2.2. Исходное ЦИ (а); результат сжатия изображения путем использования аппоксимации ранга 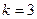(б); 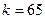(в); (г)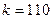

Для 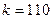визуально ЦИ неотличимо от исходного, однако выигрыш в памяти здесь значительный: для исходного – 640*480=307200 слов памяти; при 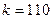- (640+480)*110=123200, т.е. почти в 3 раза.

Малоранговые аппроксимации ЦИ производят его сжатие за счет обнуления высокочастотных составляющих сигнала.