В продолжительном режиме.

Рассмотрим проводник с постоянным по длине сечением. Если

при протекании по проводнику тока мощность потерь равна P, то за

время dt в нем выделится энергия

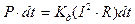. (40)

Часть этой энергии идет на нагревание проводника, а другая часть отводится в окружающую среду. Уравнение теплового баланса проводника будет иметь вид

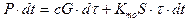. (41)

Здесь 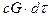– энергия, затрачиваемая на нагревание проводнка, 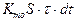– энергия, рассеиваемая в окружающую среду.

Процесс нагревания проводника характеризуется зависимостью превышения температуры проводника от времени .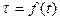

Решая уравнение (44) относительно τ, получим

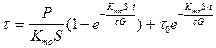(42)

Введем обозначения: 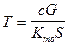и 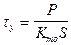, (43)

и подставим их в (42), получим уравнение, определяющее изменение температуры проводника во времени

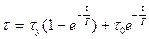. (44)

Если в начальный момент температура окружающей среды равна нулю, т.е. 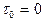, то

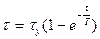. (45)

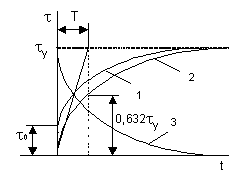
Уравнение (44) представляет собой экспоненциальную кривую 1 (рис. 27), начинающуюся в точке τ₀.Уравнение (45) описывает экспоненциальную кривую 2 для случая, когда начальная температура проводника равна температуре окружающей среды .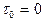

Физический смысл величин 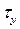и Т определяется из анализа уравнений (44) и (45). При

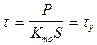. (46)

Следовательно, 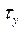– это значение

Рис. 27. Кривые нагрева проводника установившегося превышения температуры проводника над температурой окружающей среды.

Величина 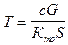называется постоянной времени, она представляет собой отношение тепловоспринимающей способности тела 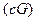к теплоотдающей способности 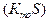. При нагревании проводника без отвода тепла в окружающую среду уравнение теплового баланса будет

,

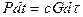отсюда 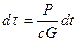. (47)

Интегрируя (47), получим

.

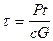Учитывая, что 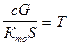, а 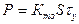, то окончательно получим

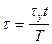. (48)

Таким образом, при K_то = 0 нагрев проводника идет по касательной к кривой 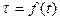в начале координат.

При .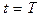

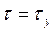Постоянную времени T можно представить как время, в течение которого проводник достиг бы установившейся температуры 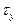, если бы отдачи тепла в окружающую среду не было. В реальных условиях, при 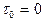и наличии теплоотдачи температура проводника за время T повысится до значения

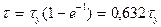. (49)

Это соотношение используют для определения величины постоянной времени, если кривая нагрева известна и получена опытным путем. На кривой нагрева находится точка 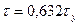и величина Т определяется отрезком, лежащим между началом координат и перпендикуляром, опущенным на ось абсцисс из этой точки. Величина постоянной времени нагрева может быть также определена величиной отрезка на прямой установившегося превышения температуры, отсекаемого касательной, проведенной из начала координат к кривой нагрева.

Процесс охлаждения проводника начнется в тот момент, когда по проводнику перестанет протекать ток. Зависимость τ = f(t) для процесса охлаждения можно получить из уравнения теплового баланса, приняв в нем Рdt = 0. Тогда, уравнение теплового баланса будет иметь вид

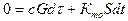. (50)

Решение этого уравнения будет

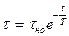. (51)

Здесь – начальное превышение температуры для процесса охлаждения. Если , то кривая охлаждения (кривая 3 на рис. 27) будет представлять собой зеркальное отражение кривой нагрева (кривая 2).