Структурное построение оптимального приёмника

Структурная схема приёмного устройства, работающего в соответствии с алгоритмом (3.18) для m=2

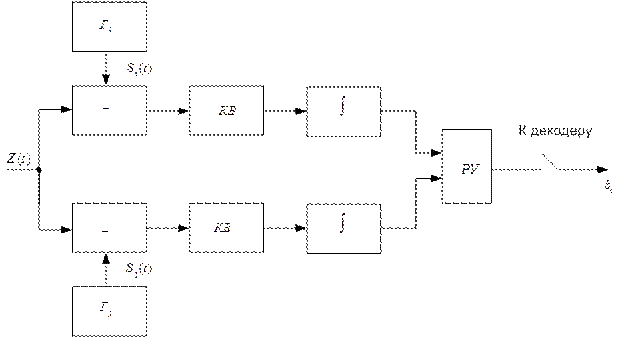
Здесь «–» - вычитающие устройства;

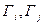– генераторы опорных сигналов ;

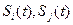«Кв» - квадраторы;

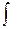– интегралы;

РУ – решающее устройство, определяющее в момент времени, кратные Т (при замыкании ключей), номер ветви с минимальным сигналом. При m>2 в схеме растёт соответственно число ветвей обработки сигнала, попадающих на РУ.

Наличие в схеме квадраторов, призванных обеспечить квадратичное преобразование мгновенных значений входных сигналов во всём их динамическом диапазоне, часто затрудняет её реализацию. Поэтому на основе (3.18) получим эквивалентный алгоритм приёма, не требующий устройств возведения в квадрат.

Раскрыв скобки под знаком интеграла и сократив в обеих частях неравенств (3.18) слагаемое 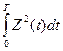, приходим к алгоритму приёма:

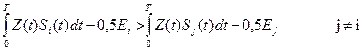(3.19)

где 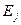– энергии ожидаемого сигнала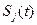

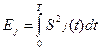(3.20)

Для двоичной системы алгоритм (13.20) сводится к проверке одного неравенства:

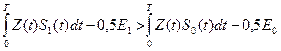(3.22)

Устройство, непосредственно вычисляющее скалярное произведение

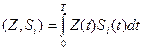(3.23)

называют активным фильтром или коррелятором; поэтому приёмник, реализующий алгоритм (3.22), называют корреляционным.

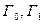На рисунке показана структурная схема приёмного устройства, работающего в соответствии с (3.22). Здесь блоки x – перемножители; – генераторы опорных сигналов 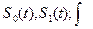– интеграторы; «–» - вычитающие устройства; РУ – решающее устройство, определяющее в моменты времени, кратные Т (при замыкании ключа), i=0, 1 – номер ветви с максимальным сигналом.

Если сигналы 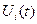выбраны таким образом, что все их реализации (а следовательно, и все реализации 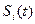) имеют одинаковые энергии ( 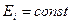), алгоритм приёма (3.22) (и соответственно его реализация) упрощается (отпадает необходимость в вычитающих устройствах) и принимает вид:

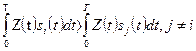(3.24)

Из (3.24) видно, что правило решения не изменится, если сигнал z(t), поступающий на вход демодулятора, умножить на любое число. Поэтому система, в которой все реализации сигнала имеют равную энергию, отличается тем, что оптимальный алгоритм приёма в ней не требует знания «масштаба» приходящего сигнала или, другими словами, знания коэффициента передачи k канала. Эта важная особенность обусловила широкое распространение систем сигналов с равной энергией, которые обычно называют системами с активной паузой. Это особенно важно для каналов с замираниями, в которых коэффициент передачи флуктуирует.

Для двоичной системы неравенство (3.22) можно представить в более простом виде:

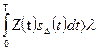, (3.25)

где 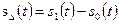– разностный сигнал; 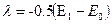– пороговый уровень. Для системы с активной паузой 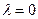, что значительно облегчает реализацию оптимальной схемы.

Существуют также системы с пассивной паузой. Реализуем алгоритм (3.25) для двоичной системы передачи однополярными импульсами (с пассивной паузой):

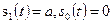. При этих сигналах 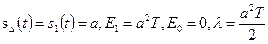и (3.25) примет следующий вид:

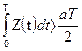(3.26)

Рассмотренную систему двоичных сигналов используют в простейших устройствах проводной связи. В радиоустройствах, а также в современных кабельных каналах связи применяют высокочастотные сигналы. Наиболее простыми двоичными системами с гармоническими сигналами являются системы с амплитудой (АМ), фазовой (ФМ) и частотной (ЧМ) манипуляцией.

В двоичной АМ 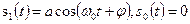. Все входящие сюда постоянные ( 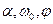) полагаем известными. Поскольку здесь 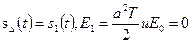, правило (3.26) запишется так:

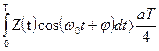
Оно реализуется схемой с блоком перемножения приходящего сигнала с опорным сигналом .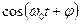

При двоичной ФМ системе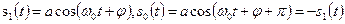

Это – система с активной паузой, и поэтому в (3.25) 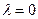. Легко убедиться, что правило решения сводится при этом к следующему: 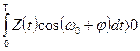– и реализуется той же схемой что двоичная АМ при 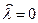. В этом случае решающее устройство играет роль дискриминатора полярностей.