Реализация алгоритма оптимального приёма на основе согласованных фильтров. Свойства согласованного фильтра

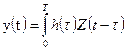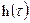Скалярное произведение (3.23) можно вычислить не только с помощью активного фильтра (коррелятора), но и с помощью пассивного линейного фильтра с постоянными параметрами. Если на вход фильтра подать принимаемый сигнал z(t), то напряжение на выходе фильтра можно выразить: , где – импульсная реакция фильтра. Выберем её такой, чтобы в момент t=Т получить y(T), совпадающее со скалярным произведением (3.23). Легко видеть, что это будет выполнено, если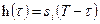

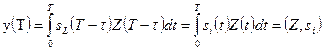(3.27)

Такой фильтр называется согласованным с сигналом 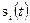. То есть фильтром, согласованным с сигналом 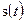, называется линейный фильтр с постоянными параметрами и импульсной реакцией:

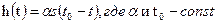(3.28)

Свойства согласованного фильтра:

1. Функция h(t) является зеркальным отображением s(t) относительно оси, проведённой через точку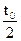

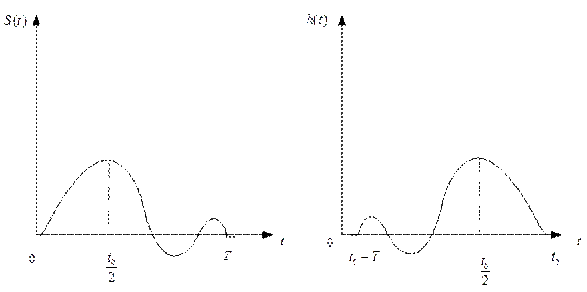
2. Если финитный сигнал S(t) поступает на вход согласованного фильтра в момент t=0 и заканчивается в момент Т, условие физической реализуемости согласованного фильтра заведомо выполняется, если момент отсчёта – постоянная 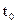удовлетворяет условию:

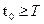(3.29)

3. Передаточная функция согласованного фильтра с импульсной реакцией (3.28)

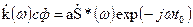, (3.30)

где 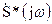– функция комплексно-сопряжённая со спектральной плотностью сигнала s(t). Следовательно, АЧХ согласованного фильтра определяется амплитудным спектром сигнала s(t), а его ФЧХ (без учёта слагаемого – 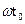, определяемого задержкой 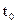) обратна по знаку фазовой характеристике сигнала s(t).

4.Если на вход фильтра подан сигнал, с которым он согласован, то сигнальная составляющая на выходе согласованного фильтра

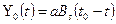(3.31)

где 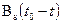– временная функция корреляции сигнала.

Согласно (3.27) в момент времени Т напряжение на выходе согласованного фильтра пропорционально сигналу на выходе интегратора активного фильтра. Поэтому оптимальный приёмник, реализующий алгоритм (3.22), может быть выполнен и на базе согласованных фильтров. Структурная схема такого приёмника для двоичной системы показана на рисунке

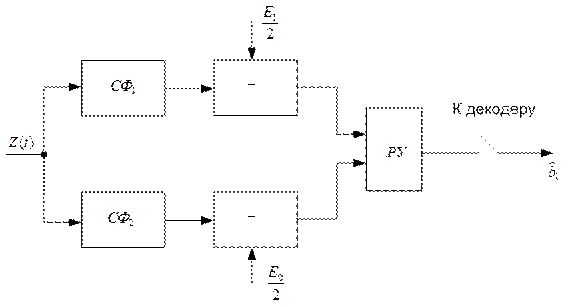
Рассмотрим ещё одно важное свойство согласованного фильтра. Будем подавать сумму детерминированного сигнала и белого шума z(t)=s(t)+N(t) на вход различных линейных цепей с постоянными параметрами и измерять в момент 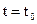отношение мгновенной мощности сигнальной составляющей к средней мощности шума на выходе цепи. Докажем, что это отношение 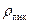максимально, если цепь является согласованным фильтром.

Пусть 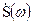– спектр входного сигнала, а 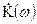– передаточная функция некоторой линейной цепи. Тогда спектр сигнальной составляющей 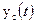на выходе цепи равен 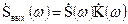. С помощью обратного преобразования Фурье найдём значение в момент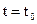

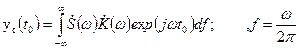(3.32)

Мощность шума (дисперсия) на выходе цепи 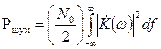. Искомое отношение 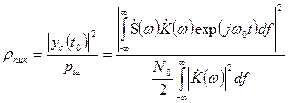(3.33)

Согласно неравенству Коши Буняковского-Шварца для любых комплексных функций A(x) и B(x) при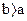

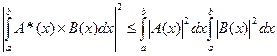, (3.34)

причём равенство имеет место только при B(x)=aA(x) (3.33), где a – произвольная постоянная. Применим неравенство Бунявского-Шварца к числителю (3.33). Если положить:

,

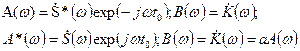то получим,

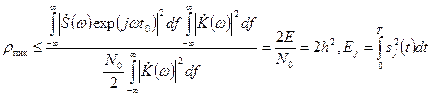, (3.35)

где 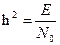– отношение энергии элемента сигнала Е на входе фильтра к спектральной плотности 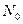белого шума.

Знак равенства согласно (3.34) и (3.35) имеет место тогда, когда передаточная функция удовлетворяет (3.30), то есть для согласованного фильтра, что и требовалось доказать. ( .)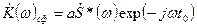

Рассмотрим возможности реализации согласованных фильтров. Согласованный фильтр для финитного сигнала произвольного вида s(t) можно, в принципе, построить на основе неискажающей длинной линии, обеспечивающей задержку сигнала на время Т, с бесконечной плотностью отводов, расположенных в дискретных точках с разносом 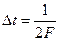, где F – эффективная ширина спектра сигнала.

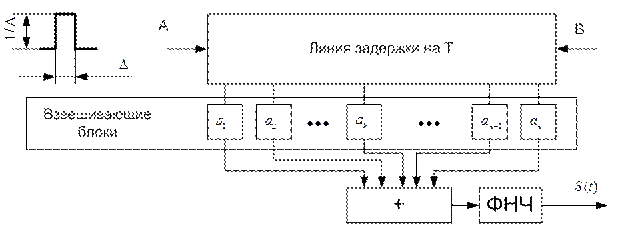
Если на вход А линии в начальный момент подаётся один короткий единичный импульс, аппроксимирующий 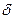– функцию, то с отводов снимаются такие же импульсы, разнесённые на интервале 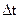, которые пройдя через взвешивающие блоки 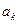, поступают поочерёдно на вход ФНЧ. Взвешивающие блоки содержат усилители с коэффициентом усиления 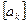, а также при отрицательных 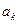-инверторы. Таким образом, приведённая схема представляет собой линейный фильтр, называемый трансверсальным с импульсной реакцией s(t). Если входной импульс подать не в точку А, а в точку B, то будет синтезирован сигнал, представляющий зеркальное отображение s(t). Поэтому та же схема со входом в точке B оказывается фильтром, согласованным с s(t).

Существуют различные другие способы реализации фильтра, точно или приближённо согласованного с сигналом заданной формы. Так, например, фильтр, согласованный с прямоугольным импульсом длительностью Т, который по определению должен иметь импульсную реакцию также в форме прямоугольного импульса, можно построить по схеме,

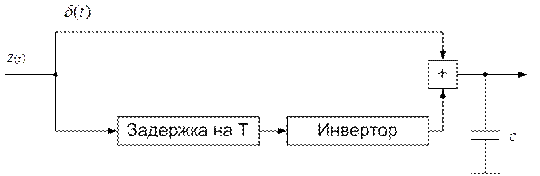
содержащей конденсатор, линию задержки на время Т, инвертор и сумматор. Если на вход этого фильтра подать единичный импульс (дельта - функцию), то он зарядит конденсатор до некоторого напряжения.

Затем спустя время Т через линию задержки и инвертор такой же входной импульс противоположной полярности поступит на конденсатор и разрядит его. Как следствие, на выходе фильтра образуется в качестве импульсной реакции прямоугольный импульс. Вариант фильтра, согласованного с прямоугольным радиоимпульсом 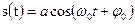, заданном на интервале (0,T), показан ниже.

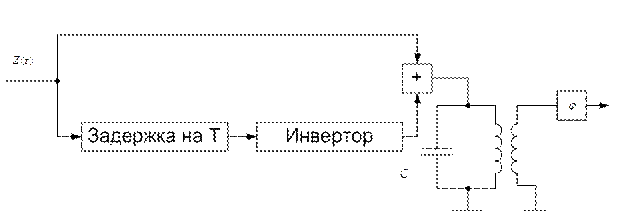Он состоит из идеального колебательного контура без потерь, настроенного на частоту 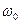и фазовращателя, сдвигающего фазу колебаний контура на – 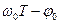. Линия задержки на Т в схеме и инвертор обеспечивают гашение колебаний фильтра вне интервала (0,T), импульсная же реакция фильтра на этом интервале с учётом фазовращателя 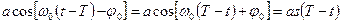, что и обеспечивает согласование.

Сравним реализации на активных фильтрах и СФ.

1. Схема с согласованными фильтрами на первый взгляд кажется проще схемы с активными фильтрами, поскольку в ней нет опорных генераторов и не возникает проблемы обеспечения их когерентности (согласование по фазе с приходящим сигналом). Однако и в схеме с согласованными фильтрами имеются свои практические трудности. В этом можно убедится, сравнив эпюры напряжений (без учёта помех в канале) на выходе фильтра (рис. Б), согласованного с прямоугольным радиоимпульсом (рис.А) и на выходе интегратора активного фильтра (рис.В).

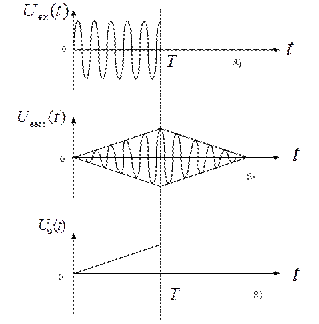
Отметим, что всюду, за исключением точки t=T, напряжения на выходах обоих фильтров отличаются друг от друга.

Из рисунков видно, что допустимая неточность во времени 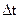снятия отсчёта максимума сигнала на выходе активного фильтра значительно больше, чем при снятии отсчёта максимума сигнала на выходе согласованного фильтра. При активном фильтре достаточно потребовать, чтобы неточность взятия отсчёта была мала по сравнению с тактовым интервалом Т, а при согласованном фильтре - по сравнению с периодом высокочастотного заполнения радиоимпульса. Трудность обеспечения когерентного отсчёта в согласованном фильтре вполне соизмерима с трудностью реализации когерентных опорных генераторов в активном фильтре.

2. В приёмниках на корреляторах легче осуществить переход на другую частоту. (В случае с СФ – нужно строить новый СФ).

Иногда в технике связи используют фильтры, характеристики которых только частично согласованы с характеристиками сигнала. Такие фильтры называются квазиоптимальными.