Дискретное преобразование Фурье
Исследуем особенности спектрального представления дискретного сигнала, который задан на отрезке [0,T] своими отсчётами 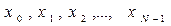 , взятыми соответственно в моменты времени
, взятыми соответственно в моменты времени 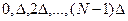 , полное число отсчётов
, полное число отсчётов 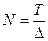 (
( 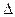 - интервал дискретизации)
- интервал дискретизации)
Методика изучения таких дискретных сигналов состоит в том, что полученная выборка отсчётных значений мысленно повторяется бесконечное число раз. В результате сигнал становится периодическим.
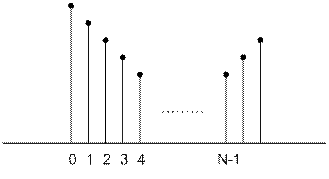
Сопоставив такому сигналу некоторую математическую модель можно воспользоваться разложением в ряд Фурье и найти соответствующие амплитудные коэффициенты. Совокупность этих коэффициентов образует спектр дискретного периодического сигнала.
Воспользуемся моделью в виде последовательности дельта-импульсов. Тогда исходное колебание x(t) будет выражено формулой
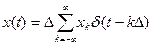 (7.1)
(7.1)
Где 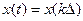 – выборочные значения аналогового сигнала.
– выборочные значения аналогового сигнала.
Представим этот сигнал комплексным рядом Фурье.
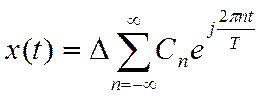 (7.2)
(7.2)
С коэффициентами:
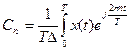 (7.3)
(7.3)
Подставляя формулу (7.1) в (7.3) получим
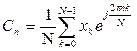 - дискретное преобразование Фурье (ДПФ) (7.4)
- дискретное преобразование Фурье (ДПФ) (7.4)
Основные свойства ДПФ
1. ДПФ- линейное преобразование т.е. сумме сигналов отвечает сумма их ДПФ
2. Число различных коэффициентов 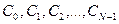 вычисляемых по формуле (7.4) равно числу N за период; при n=N коэффициент
вычисляемых по формуле (7.4) равно числу N за период; при n=N коэффициент 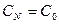
3. Коэффициентов 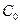 (постоянная составляющая) является средним значением всех отсчётов:
(постоянная составляющая) является средним значением всех отсчётов:
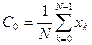
4. Если N- чётное число, то
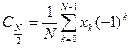
5. Пусть отсчётные значения 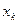 – вещественные числа. Тогда коэффициенты ДПФ, номера которых располагаются симметрично относительно N/2, образуют сопряжённые пары:
– вещественные числа. Тогда коэффициенты ДПФ, номера которых располагаются симметрично относительно N/2, образуют сопряжённые пары:
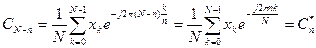
Задача дискретного спектрального анализа может быть поставлена и по-иному. Допустим, что коэффициенты 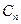 , образующие ДПФ, заданы. Положим в формуле (7.2)
, образующие ДПФ, заданы. Положим в формуле (7.2) 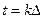 и учтём что суммируется лишь конечное число членов ряда, которые отвечают гармоникам, содержащимся в спектре исходного сигнала.
и учтём что суммируется лишь конечное число членов ряда, которые отвечают гармоникам, содержащимся в спектре исходного сигнала.
Таким образом получаем формулу для вычисления отсчётных значений
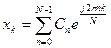 - обратное дискретное преобразование
- обратное дискретное преобразование
Фурье (ОДПФ) (7.5)
Пример:
Дискретный сигнал на интервале своей периодически задан шестью равноотстоящими отсчётами 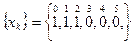
Найти коэффициенты ДПФ этого сигнала
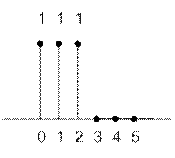
k – номер отсчёта
n – номер гармоники
1) 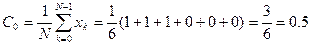
2)
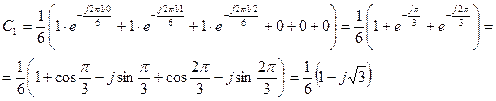
3)
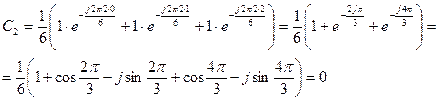
4)
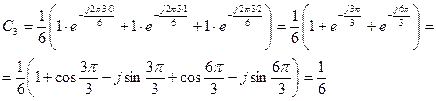
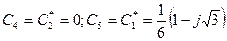
Дата добавления: 2016-07-22; просмотров: 2091;











