Тема 2.2 Формулы логики.

Алфавитом называется любой непустой набор символов. Элементы этого набора называются символами алфавита.

Словом в алфавите 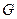называется произвольная конечная (возможно пустая) последовательность символов из 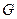. Фиксируем некоторый конечный или счетный алфавит переменных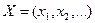

Формула алгебры логики определяется следующим образом (индуктивное определение):

· Любая логическая переменная есть формула.

· Если 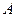- формула, то 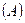- формула (допустимы технические символы)

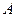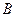· Если и – формулы, то 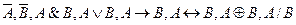– тоже формулы (допустимы все логические связки).

· Других формул нет.

Подформулой формулы 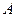называется любое подслово слова 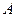, которое само является формулой.

Для сокращения записи формул обычно принимаются следующие соглашения:

· если часть формулы заключена в скобки, то сначала производится действие в скобках,

· если над частью формулы стоит знак отрицания, то он заменяет собой скобки, в которые заключена эта часть формулы.

Принят следующий порядок выполнения операций:

· Отрицание

· конъюнкция,

· дизъюнкция,

· импликация и эквивалентность в порядке их записи,

Формула называется тождественно истинной или тавтологией, если она реализует функцию «тождественная единица», и тождественно ложной, если 0.

Являются ли формулы тождественно истинными:

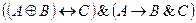
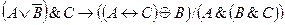
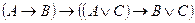
Формулы логики, принимающие всегда ложное значение, называются тождественно ложными (или противоречиями).

Например, формула 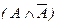- противоречие.

Формулы алгебры логики, принимающие значение «ложь» хотя бы на одном наборе значений атомов, входящих в формулу называются опровержимыми.

Формулы алгебры логики, принимающие значение «истина» хотя бы на одном наборе значений атомов, входящих в формулу называются выполнимыми.

Формулы Р и Q называются равносильными, если их истинностные значения совпадают при любом выборе истинностных значений атомов, входящих в эти формулы.

Запись Р 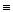Q означает, что формулы Р и Q равносильны