Тема 2.1 Основные логические операции.
Высказывание – это предложение которое может быть либо истинным, либо ложным.
В математической логике не рассматривается сам смысл высказываний, определяется только его истинность или ложность, что принято обозначать соответственно И или Л.
Понятно, что истинные и ложные высказывания образуют соответствующие множества. С помощью простых высказываний можно составлять более сложные, соединяя простые высказывания союзами “и”, “или”.
Введем множество 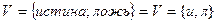
Над высказываниями можно выполнять следующие операции:
1. ┐ (не) – одноместная операция отрицания;
2. 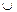 (или) – двуместная операция дизъюнкция;
(или) – двуместная операция дизъюнкция;
3. 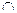 (и) – двуместная операция конъюнкция;
(и) – двуместная операция конъюнкция;
4. 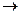 (если, то) – двуместная операция импликация;
(если, то) – двуместная операция импликация;
Каждая операция характеризуется своей таблицей истинности:
Вводятся следующие логические операции (связки) над высказываниями
1) Отрицание. Отрицанием (логическим “не”) высказывания Р называется высказывание, которое истинно только тогда, когда высказывание Р ложно.
Обозначается 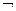 Р или
Р или 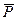 .
.
Соответствие между высказываниями определяется таблицами истинности. В нашем случае эта таблица имеет вид:
| P | 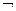 Р Р
|
| И | Л |
| Л | И |
2) Конъюнкция. Конъюнкцией (логическим “и”) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания.
Обозначается P&Q или Р 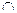 Q.
Q.
| P | Q | P 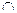 Q Q
|
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
3) Дизъюнкция. Дизъюнкцией (логическим “или”) двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны.
Обозначается P 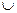 Q.
Q.
| P | Q | P 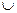 Q Q
|
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
4) Импликация. Импликацией (логическим следованием) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда высказывание Р истинно, а Q – ложно.
Обозначается PÉQ (или Р 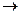 Q). Высказывание Р называется посылкой импликации, а высказывание Q – следствием.
Q). Высказывание Р называется посылкой импликации, а высказывание Q – следствием.
| P | Q | P 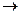 Q Q
|
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
5) Эквиваленция. Эквиваленцией (логической равносильностью) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинности высказываний совпадают.
Обозначается Р~Q или РÛQ.
| P | Q | P~Q |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | И |
С помощью этих основных таблиц истинности можно составлять таблицы истинности сложных формул.
Построим истинностную таблицу сложного высказывания:
S=(A→B)∧( ┐C)∨(A↔C)
Очевидно, истинностная таблица будет содержать 23 = 8 строк.
Скобки применяются, если нарушаются естественный порядок операций: отрицание, конъюнкция, дизъюнкция, импликация, двойная импликация. Скобки (А→В) указывают на то, что сначала нужно выполнить
импликацию, затем найти (А→В)∧С. Скобки в выражении (A↔C) можно опустить. Заключительной операцией в построении истинностной таблицы для S будет дизъюнкция двух высказываний: (А→В)∧С и (A↔C).
Таблица
| А | В | С | А→В | (А→В)∧С | ┐С | A↔C | C (A↔C) | |
Итак, формула S задает высказывание которое истинно на следующих наборах значений элементарных высказываний:
А=1 В=1 С=1 (все три элементарных высказывания истинны)
А=1 В=0 С=1 (А, С - истинны, В - ложно )
А=0 В=1 С=1 (А - ложно, В и С - истинны)
А=0 В=1 С=0 (В - истинно, А и С - ложны)
А=0 В=0 С=1 (С - истинно, А и В - ложно)
А=0 В=0 С=0 (все три высказывания ложны).
Высказывательной формой называется: 1. любая переменная (она в свою очередь называется элементарной (автомарной) высказывательной формой); 2. если 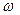 и
и 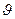 высказывательные формы, то и их отрицания,
высказывательные формы, то и их отрицания, 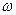
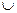
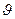 ,
, 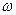
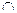
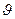 ,
, 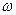
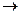
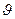 ,
, 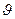
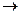
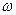 , также являются высказывательными формами.
, также являются высказывательными формами.
Дата добавления: 2016-07-22; просмотров: 2238;











