Тема 1.3 Свойства операций.
Операции над множествами обладают некоторыми свойствами. Эти свойства выражаются совокупностью тождеств, справедливых независимо от конкретного содержания входящих в них множеств.
1. транзитивность операции включения:
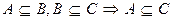
т.е. если множество А является подмножеством В, а множество В является подмножеством множества С, то множество А является подмножеством множества С.
2. дистрибутивность операции пересечения относительно объединения:
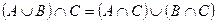
т.е. если множество А объединить с множеством В, а потом пересечь с множеством С, то это тоже самое, что А пересечь с С и В пересечь с С, а потом объединить их.
3. дистрибутивность операции объединения относительно пересечения:
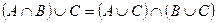
т.е. если множество А пересечь с множеством В, а потом объединить с множеством С, то это тоже самое, что А объединить с С и В объединить с С, а потом пересечь их.
4. первый закон двойственности:
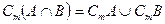
т.е. дополнение множества 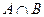 , есть не что иное, как объединение дополнения множества А и дополнения множества В.
, есть не что иное, как объединение дополнения множества А и дополнения множества В.
5. второй закон двойственности:
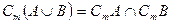
т.е. дополнение множества 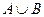 , есть пересечение их дополнений.
, есть пересечение их дополнений.
6. ассоциативность операции объединения:
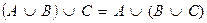
7. ассоциативность операции пересечения:
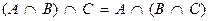
8. свойства операции объединения:
· коммутативность объединения:
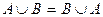 ,
,
· 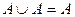 ,
,
· 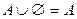 ,
,
· 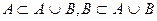 .
.
9. свойства операции пересечения:
· коммутативность пересечения:
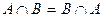 ,
,
· 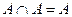 ,
,
· 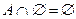 ,
,
· 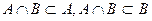 .
.
10. свойства операции разности:
· 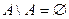 ,
,
· 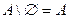 ,
,
· 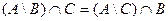 ,
,
·  ,
,
· 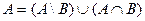 .
.
11. дополнение к дополнению любого множества есть всегда само множество, т.е. 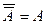
12. 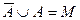
13. 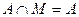
Тест
1. Будет ли пустое множество V каким-либо подмножеством некоторого множества?
а) будет собственным подмножеством;
б) будет несобственным подмножеством;
в) не будет никаким подмножеством.
2. Что есть множество А\В, если А - множество всех книг в библиотеке МЭСИ по различным отделам науки и искусства, а В – множество всех книг во всех библиотеках России?
а) множество математических книг в России без математических книг в МЭСИ;
б) множество книг по искусству в библиотеке МЭСИ;
в) множество книг в библиотеке МЭСИ по искусству и науке, кроме математических.
3. Совпадают ли дистрибутивные законы Булевой алгебры и алгебры действительных чисел;
а) оба совпадают;
б) оба не совпадают;
в) один совпадает, другой - нет.
4. Есть ли законы для дополнений в алгебре действительных чисел?
а) да;
б) нет;
в) некоторые есть, некоторых нет.
5. Справедливы ли законы идемпотентности Булевой алгебры в алгебре действительных чисел?
а) справедливы;
б) несправедливы;
в) один справедлив, другой нет.
6. Обладают ли свойством двойственности формулы поглощения?
а) да;
б) нет;
в) одна обладает, другая нет.
7. Можно ли поставить в соответствие единицу или ноль соответственно универсальному и пустому множеству, исходя из свойств операций?
а) можно;
б) единицу - можно, ноль - нет;
в) ноль - можно, единицу - нет.
8. Обладают ли формулы склеивания свойством двойственности
а) нет;
б) да;
в) одна обладает, другая нет.
9. Будет ли каждое из множеств А, В, С, D подмножеством другого, если А - множество действительных чисел, В - множество рациональных чисел, С - множество целых чисел, D - множество натуральных
чисел.
а) да;
б) нет;
в) лишь некоторые из множеств являются подмножествами перечисленных множеств
Контрольная работа
1 Вариант
1. А={х | х 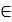 N : х-однозначное, составное число}
N : х-однозначное, составное число}
В={7,8,13}
Определить количество подмножеств у множества А. Выписать все подмножества у множества В.
2. Х={ однозначные натуральные числа, кратные 3}
Y={1,3,5,6,8}
Найти: Х 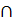 Y, X
Y, X 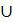 Y, X\Y, Y\X
Y, X\Y, Y\X
3. А=(-1,8]; В=[0,12]
Найти: А\В, В\А, В\(А 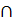 В), A\(A
В), A\(A 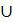 B)
B)
4. Доказать: А 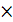 (В\С)=(А
(В\С)=(А 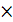 В)\(А
В)\(А 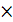 С)
С)
5. Упростить: (А 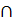 В)
В) 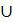 (
( 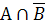 )U (
)U ( 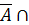 В)
В)
2 Вариант
1. А={х | x 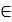 N : х-однозначное простое число}
N : х-однозначное простое число}
В={0,3,21}
Определить количество подмножеств у множества А. Выписать все подмножества у множества В.
2. Х={ Однозначное натуральное число : 4}
Y={2,3,4,5,6,8,11}
Найти: Х 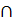 Y, X
Y, X 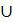 Y, X\Y, Y\X
Y, X\Y, Y\X
3. А=[2,14]; В=(-3,10]
Найти: А\В, В\А, В\(А 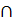 В), A\(A
В), A\(A 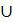 В)
В)
4. Доказать: 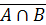 =
= 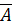 U
U 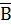
5. Упростить: (А 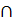 В)
В) 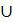 (
( 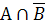 )(
)( 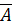
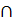 В)
В)
Дата добавления: 2016-07-22; просмотров: 2400;











