Измерение связи номинальных признаков
Учеными ряда стран за последние 100 лет разработано несколько методов измерения связи таких признаков. Описательные признаки - обычно альтернативные признаки, при которых каждый имеет по две разновидности. Например, больные могут выздороветь, а могут не выздороветь, признак есть (нет).
Коэффициент взаимной сопряженности Бравайса.В тех случаях, когда находящиеся в связи явления представлены описательными величинами, коэффициент корреляции находят по следующей формуле.
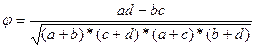 , где a,b,c,d - количество случаев отдельных комбинаций разновидностей исследуемых явлений.
, где a,b,c,d - количество случаев отдельных комбинаций разновидностей исследуемых явлений.
При вычислении коэффициента корреляции знаменатель формулы всегда имеет положительный знак. Знак перед r зависит от того, какое из произведений больше ad или bc. Для того чтобы легче вычислить коэффициент корреляции, пользуются так называемой четырехпольной таблицей. В первом столбце этой таблицы указывают обе разновидности одного явления - Х1 и Х2, а в первой строке - обе разновидности второго -Y1 и Y2. При этом X1 и Y2 обозначают положительные разновидности, а X2 и Y1 - отрицательные. В указанных выше примерах под положительными разновидностями подразумевают выздоровевших, получивших отравление. При таком состоянии четырехпольная таблица принимает следующий вид:
| X | Y1 | Y2 | Всего |
| X1 | a | B | (a+b) |
| X2 | c | D | (c+d) |
| Всего | (a+c) | (b+d) | (a+b+c+d) |
Пример: Имеются следующие данные о вакцинации против гриппа и заболеваемости гриппом во время эпидемии:
| Заболело | Не заболело | Всего | |
| Вакцинировано | 10 | 490 | 500 |
| Не вакцинировано | 990 | 510 | 1500 |
| Всего | 1000 | 1000 | 2000 |
Требуется определить размер связи между проведенной вакцинацией и заболеваемостью.r=-0,6. Коэффициент корреляции показывает обратную связь: вакцинированные реже болеют, чем не вакцинированные.
Коэффициент сопряженности Чупрова.Дальнейшим обоб-щением четырехпольных таблиц являются многопольные таблицы, для которых сопряженность наиболее часто оценивается по формуле, предложенной русским статистиком А. А. Чупровым. Прежде чем приводить ее рассмотрим несколько реальных ситуаций, когда такая оценка может потребоваться. Известно, например, что окраска тюльпанов связана с наличием определенных пигментов. Может представлять интерес вопрос о том, с какими именно пигментами преимущественно связана та или иная окраска цветка. Или другой пример. Окружающая гнездо полярной крачки обстановка может представлять собой зеленые растения, растения и гальку, пестрые камешки и т. д. При этом можно наблюдать самые разные по качеству гнезда: от его отсутствия до очень хорошо сделанного. В этом случае желательно знать, связано ли качество гнезда с какой-то одной или несколькими характеристиками окружающей среды. Общим для этих и других подобных задач является то, что в распоряжении экспериментатора оказываются данные о некотором множестве объектов, обладающих двумя признаками, причем каждый из признаков может иметь несколько градаций. В этом случае 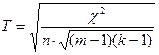 , где m - число разновидностей явления Х; k - число разновидностей явления Y, n – общее число объектов (m*k).
, где m - число разновидностей явления Х; k - число разновидностей явления Y, n – общее число объектов (m*k).
Независимо то того, что каждый из описательных признаков, несмотря на разницу в численности его разновидностей, можно свести к альтернативному - только с двумя разновидностями, довольно часто в практике возникает необходимость работать с описательными признаками более двух разновидностей. В таких случаях необходимо при вычислении коэффициента корреляции составлять так называемую корреляционную таблицу (где X1,X2,...Xn - обозначают разновидность одного признака, а Y1, Y2... Yn - разновидности другого).
При наличии такой схемы коэффициент корреляции находят по формуле: 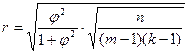 , где
, где 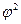 - коэффициент связи, m- число разновидностей явления Х; k - число разновидностей явления Y.
- коэффициент связи, m- число разновидностей явления Х; k - число разновидностей явления Y.
Данный метод пригоден также и для экспрессной оценки связи между количественными (например возраст) и качествен-ными (например брак) параметрами.
На практике (особенно в зоологии и ботанике) довольно часто встречаются другие меры измерения связи.
| Коэффициент Жаккара | 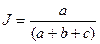
|
| Простой коэффициент втречаемости (показатель подобия Сокала и Миченера) | 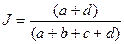
|
| Показатель подобия Рассела и Рао | 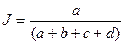
|
| Коэффициент ассоциации Юла | 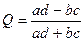
|
| Хеммингово расстояние | H=a+d |
| Коэффициент детерминации | R=r2 |
| Коэффициент определения | R=100r2 |
| Коэффициент акорреляции | 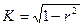
|
Дата добавления: 2020-10-01; просмотров: 602;











