Измерение связи количественных признаков
В случае, когда параметры измеряются количественно, теснота парной линейной корреляционной связи может быть измерена корреляционным отношением:
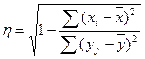 .
.
Кроме того, при линейной форме уравнения применяется и другой показатель тесноты связи - коэффициент корреляции rxy. Этот показатель представляет собой стандартизованный коэф-фициент регрессии, т.е. коэффициент выраженный не в абсолют-ных единицах измерения признаков, а в долях среднего квадратичного отклонения результирующего признака:
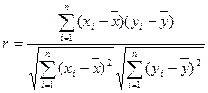 .
.
Коэффициент корреляции был предложен английским статистиком Пирсоном. Его интерпретация такова: отклонение признака-фактора от его среднего значения на величину своего среднего квадратичного отклонения в среднем по совокупности приводит к отклонению признака-результата от своего среднего значения на Rxy его среднего квадратичного отклонения.
Для интерпретации коэффициента корреляции необходимо знать область его существования 0<=|r|<=1. Как ясно из формулы, минимальное, именно нулевое значение коэффициента корреляции может быть достигнуто, если положительные и отрицательные произведения отклонений признаков от их средних величин в числителе уравновесят друг друга. Это свидетельствовало бы о полном отсутствии связи, но вероятность такого абсолютно точного взаимопогашения абсолютно мала для любой реальной, но бесконечно большой совокупности. Поэтому и при отсутствии реальной связи коэффициент корреляции на практике не равен 0. Максимально тесная связь - это связь функциональная.
Дата добавления: 2020-10-01; просмотров: 515;











