Корреляционный анализ

Различают два типа связей между различными явлениями и их признаками: функциональную или жестко детерминированную, с одной стороны, и статистическую или стохастически детерминированную, с другой. Строго определить различие этих двух типов связи можно тогда, когда они получают математическую формулировку. Для простоты будем говорить о связи двух явлений или двух признаков, математически отображаемой в форме уравнения связи двух переменных.

Если с изменением значения одной из переменных вторая изменяется строго определенным образом, т. е. значению одной переменной соответствует одно или несколько точно заданных значений другой переменной, связь между ними является функциональной.

Нередко говорят о строгом соответствии лишь одного значения второй из переменных каждому значению первой из них, но это неверно. Например, связь между x и y является строго функциональной если y=√x; но значению x=4 соответствует не одно, а два значения; y₁=2 и y₂=-2. Уравнения более высоких степеней могут иметь несколько корней, связь разумеется остается функциональной.

Функциональная связь двух величин возможна лишь при условии, что вторая из них зависит только от первой и ни от чего более. В реальной природе таких связей нет; они являются лишь абстракциями, полезными и необходимыми при анализе явлений, но упрощающими реальность. Функциональная зависимость данной величины y от многих факторов x₁, x₂, ... x_k возможна только в том случае, если величина y всегда зависит только от переменного набора факторов x₁, x₂, ... x_k и ни от чего больше. Между тем все явления и процессы реального мира связаны между собой, и нет такого конечного числа переменных k, которые абсолютно полно определяли бы собой зависимую величину y. Следовательно, множественная функциональная зависимость переменных есть тоже абстракция, упрощающая реальность.

Однако в науке успешно используют представление связей как функциональных не только в аналитических целях, но нередко и в целях прогнозирования. Это возможно потому, что в некоторых простых системах интересующая нас переменная зависит в основном (скажем на 99% или даже на 99.99%) от немоногих других переменных или только от одной переменной. То есть связь в такой несложной системе является хотя и не абсолютно функциональной, но практически очень близкой к таковой.

Длина года (период обращения Земли вокруг Солнца) почти функционально зависит только от массы Солнца и расстояния Земли от него. На самом деле она зависит в очень слабой степени и от масс, и расстояния других планет от Земли, но вносимые ими (и тем более в миллионы раз более далекими звездами) искажения функциональной связи для всех практических целей, кроме космонавтики, пренебрежимо малы.

Статистическая связь не имеет ограничений и условий, присущих функциональной связи. Если с изменением значения одной переменной вторая может в определенных пределах принимать любые значения с вероятностями, но ее среднее значение или иные статистические (массовые) характеристики изменяются по определенному закону - связь является статистической. Иными словами, при статистической связи разным значениям одной переменной соответствуют разные распределения значений другой переменной.

Корреляционной связью называют важнейший частный случай статистической связи, состоящий в том, что различным значениям одной переменной соответствуют различные средние значения другой. С изменением значения x закономерным образом изменяется среднее значение признака y; в то время как в каждом отдельном случае значение признака y (с различными степенями вероятности) может принимать множество различных значений.

Если же с изменением значения признака x среднее значение признака y не изменяется закономерным образом, но закономерно изменяется другая статистическая характерис-тика (показатели вариации, асимметрии, эксцесса и т.п.), то связь является не корреляционной, а статистической.

Статистическая связь между двумя признаками (переменными величинами) предполагает, что каждый из них имеет случайную вариацию индивидуальных значений относительно средней величины. Если же такую вариацию имеет лишь один из признаков, а значения другого являются строго детерминированными, то говорят лишь о регрессии, но не о статистической (тем более корреляционной) связи.

При анализе динамических рядов можно измерять регрессию уровней ряда урожайности (имеющих случайную изменчивость) на номера лет. Но нельзя говорить о корреляции между ними и применять показатели корреляции с соответствующей им интерпретацией.

Само слово корреляция ввел в употребление в статистику английский биолог и статистик Френсис Гальтон в конце XIX века. Тогда оно писалось как “corelation” (соответствие), но не просто “связь” (relation), а “как бы связь”, т.е. связь, но не в привычной функциональной форме. В науке вообще, а именно в палеонтологии, термин “корреляция” применял еще раньше, в конце XVIII века французский палеонтолог Жорж Кювье. Он ввел даже “закон корреляции” частей и органов животных. “Закон корреляции” помогает восстановить по найденным в раскопках черепу, костям и т.д. облик всего животного и его место в системе: если череп с рогами, то это было травоядное животное, а его конечностями были копыта; если же лапа с когтями - то хищное животное без рогов, но с крупными клыками.

Например, измеряем рост и вес человека, каждое измерение представлено точкой в двумерном пространстве:

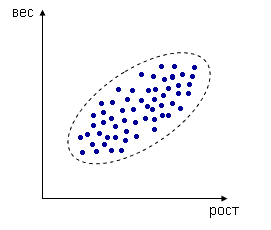
Несмотря на то, что величины носят случайный характер, в общем наблюдается некоторая зависимость - величины коррелируют.

В данном случае это положительная корреляция (при увеличении одного параметра второй тоже увеличивается). Возможны также такие случаи:

Отрицательная корреляция:

Отсутствие корреляции:

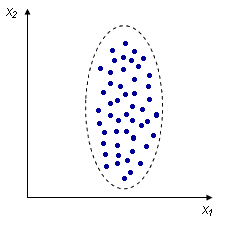
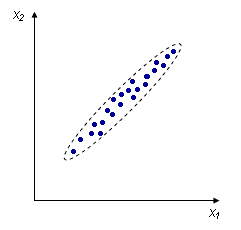
Взаимосвязь между переменными необходимо охарактеризовать численно, чтобы, например, различать такие случаи:

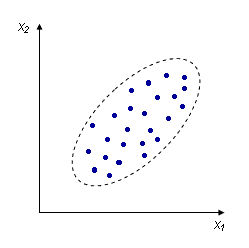
Корреляционная связь между признаками может возникать различными путями:

1. Важнейший путь - причинная зависимость результативного признака (его вариации) от вариации факторного признака. Например, признак x - балл оценки плодородия почв, признак y - урожайность сельскохозяйственной культуры. Здесь совершенно ясно логически, какой признак является независимой переменной (фактор) x, какой - зависимой переменной (результат) y.

2. Совершенно иная интерпретация нужна при изучении корреляционной связи между двумя следствиями одной причины. Известен классический пример, приведенный крупнейшим статистиком России начала XXв А.А. Чупровым: если в качестве признака x взять число пожарных команд в городе, а за признак y - сумму убытков за год в городе от пожаров, то между признаками x и y в совокупности городов России существенная прямая корреляция; в среднем, чем больше пожарников в городе, тем больше и убытков от пожаров. Уж не занимались ли поджигательством из боязни потерять работу? Но дело в другом. Данную корреляцию нельзя интерпретировать как связь причины и следствия; оба признака - следствия общей причины - размера города. Вполне логично, что в крупных городах больше пожарных частей, но и больше пожаров, и убытков от них за год, чем в мелких городах.

3. Третий путь возникновения корреляции - взаимосвязь признаков, каждый из которых и причина и следствие. В биологии примером таких взаимосвязей являются механизмы биологических обратных связей между параметрами организма при поддержании гомеостаза.