Относительный риск. Отношение шансов
| Исход есть (1) | Исхода нет (0) | Всего | |
| Фактор риска есть (1) | 10 (А) | 13 (В) | 23 (А+В) |
| Фактора риска нет (0) | 4 (С) | 21 (D) | 25 (С+D) |
| Всего |
Мы рассмотрели способы проверки гипотез о наличии статистической связи между номинальными переменными, а также способы оценки силы взаимосвязи между этими переменными. Тем не менее сообщение о том, что была обнаружена статистически значимая связь средней силы между фактором риска и исходом, для исследователей в области биомедицинских наук, заинтересованных в практическом применении результатов исследования, недостаточно информативно. Гораздо продуктивнее было бы говорить о количественной оценке вероятности исхода, связанной с наличием фактора риска. Однако не все исследования позволяют говорить о риске и оценивать вероятность возникновения исхода в зависимости от наличия или отсутствия фактора риска.
Мы же остановимся только на некоторых расчетах, применимых к нашему примеру. Учитывая, что наше гипотетическое исследование было проспективным, мы можем рассчитать относительный риск (Relative Risk, RR). Поскольку в примере ничего не сообщается о времени наблюдения, но подразумевается, что оно было одинаковым для обеих групп (с наличием фактора риска и без него), относительный риск будет равен отношению рисков. Отношение рисков отражает, во сколько раз риск исхода при наличии фактора риска выше риска исхода при отсутствии фактора риска и рассчитывается применимо к таблице следующим образом:
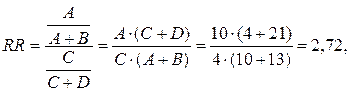
Это говорит о том, что фактор риска может увеличивать вероятность возникновения исхода в 2,7 раза или что риск исхода у тех, у кого есть фактор риска, в 2,7 раза выше, чем у тех, у кого фактора риска нет. Такой результат гораздо более информативен. Однако различия в 2,7 раза справедливы только для нашей выборочной совокупности. Даже если допустить, что наша выборка репрезентативна, систематические ошибки отсутствуют, а влияние вмешивающихся факторов (конфаундеров) минимально, относительный риск для генеральной совокупности может отличаться, поэтому всегда рекомендуется представлять интервальную оценку относительного риска с помощью 95 % доверительного интервала. Этот интервал представляет собой область, в которую попадает истинное значение доли в 95 % случаев. Другими словами, можно с 95 % надежностью сказать, что истинное значение частоты встречаемости признака в генеральной совокупности будет находиться в пределах 95 % доверительного интервала. Методы расчета доверительного интервала для частот и долей рассматривались в предыдущем номере журнала [4]. Для относительного риска 95 % доверительный интервал можно рассчитать по формуле:
Верхняя граница: ex, где
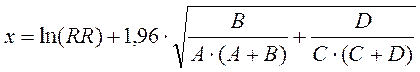
Нижняя граница: ех, где
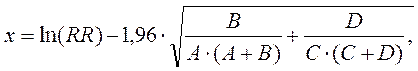
а е – основание натурального логарифма (число Эйлера ~ 2,7). Для данного примера можно с 95 % уверенностью сказать, что относительный риск будет находиться в промежутке от 1,0 до 7,5. Значительная ширина доверительного интервала вызвана малым объемом выборки. Хотелось бы предостеречь читателей от переоценки важности относительного риска. Например, относительный риск может быть равен 2,0 как в ситуации, когда абсолютные риски развития заболевания равны 1 на 1 000 000 и 2 на 1 000 000, а также 1 на 10 и 2 на 10. В первом случае абсолютная разница рисков будет не очень важна, так как составит 0,000 001. Во втором же разница рисков составит 0,1. Если взять обратные величины из полученных разностей рисков, то можно будет увидеть у скольких человек необходимо устранить фактор риск, чтобы предотвратить 1 исход. В первом случае надо устранить фактор риска у миллиона, а во втором – всего у 10 человек. Особенно актуальными такие расчеты становятся при оценке эффективности лечебного вмешательства. Рассчитанная величина будет называться числом пациентов, подвергаемых лечению, на один предотвращенный неблагоприятный исход (в англоязычной литературе NNT – Number Needed to Treat).
Для нашего примера тоже можно рассчитать разность рисков: А(А+В)/С(С+D), которая будет равна 0,275, или 27,5 %, а для того, чтобы предотвратить один исход, необходимо устранить фактор риска всего у 4 человек (NNT ~3,6), что говорит о том, что потенциальный эффект от профилактических мер, направленных на устранение изучаемого фактора риска, очень велик (при условии, что распространенность фактора риска в генеральной совокупности такая же, как и в выборке).
Если бы наше исследование было типа «случай – контроль», было бы неверным рассчитывать относительный риск. В таких исследованиях в качестве меры эффекта выступает отношение шансов (Odds Ratio, OR). Представим на минуту, что наше исследование было исследованием типа «случай – контроль». Тогда
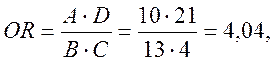 то есть шансы на изучаемый исход были в 4 раза выше у тех участников исследования, у кого имелся фактор риска, чем у тех, у кого фактора риска не было. При проецировании результатов на генеральную совокупность также необходимо рассчитать 95 % доверительный интервал, в который попадут значения
то есть шансы на изучаемый исход были в 4 раза выше у тех участников исследования, у кого имелся фактор риска, чем у тех, у кого фактора риска не было. При проецировании результатов на генеральную совокупность также необходимо рассчитать 95 % доверительный интервал, в который попадут значения
от 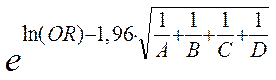
до 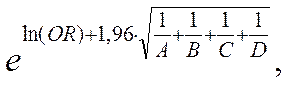
где е – основание натурального логарифма. Для нашего примера 95 % значений отношения шансов (ОШ) будут попадать в интервал от 1,0 до 15,6. Следует помнить, что вышеприведенные формулы для расчета доверительных интервалов предназначены только для независимых данных и неприменимы в исследованиях типа «до – после», а также в исследованиях типа «случай – контроль» по методу подобранных пар (Matched case-control study). Не стоит представлять в одном исследовании и относительный риск, и отношение шансов в одном и том же исследовании. Для исследований типа «случай – контроль» описанные выше расчеты относительного риска, разницы рисков и NNT провести невозможно.
Дата добавления: 2020-10-01; просмотров: 696;











