Метод наименьших квадратов
Метод наименьших квадратов, разработанный знаменитыми математиками К. Гауссом и А. Лежандром, берет свое начало от задач геодезии и астрономии. Рассмотрим его существо на примере линейной модели. Итак, пусть для представления полученных данных мы выбрали линейную модель y*=a+bx, где х – независимая переменная, т. е., переменная, которую экспериментатор может менять по своему усмотрению; y* - зависимая переменная или отклик; a и b – коэффициенты (параметры). Из данных, приведенных в примере, видно, что именно такой моделью (уравнением прямой линии) может быть описана зависимость.
С другой стороны, видно что реально наблюдаемые значения отклика yi несколько отличаются от откликов yi*, соответствующих уравнению модели. И такое положение будет всегда, даже в тех случаях, когда зависимая и независимая переменные будут связаны строгой функциональной зависимостью. В этом случае отклонения эмпирических значений от теоретических связаны с погрешностями измерений, которые всегда имеют место.
Итак, каждому значению независимой переменной в общем случае соответствует ошибка: ei=yi-yi*.
Естественно, что в зависимости от того, как будет проведена прямая, аппроксимирующая набор экспериментальных данных, величины ei будут различны. Именно, для того, чтобы избежать субъективности при построении эмпирической модели, и был разработан метод наименьших квадратов, позволяющий однозначно определить параметры выбранной модели. В основе этого метода лежит критерий минимизации суммы квадратов ошибок, т. е. требование, чтобы  была минимальной.
была минимальной.
Покажем, как используется метод наименьших квадратов на примере оценки параметров для уравнения y*=a+bx.
В общем случае необходимо решить систему уравнений:
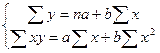 , из которых находятся коэффициенты a и b.
, из которых находятся коэффициенты a и b.
Подставляя данные из примера, получаем:
16,3=7a+56b
107=56a+560b
Откуда a=4, b=-0,209.
В таблице приведено сравнение между реальными и теоретическими данными, а также величины ошибок.
| Y | 3,6 | 2,9 | 3,2 | 1,8 | 2,3 | 1,7 | 0,8 |
| y* | 3,582 | 3,164 | 2,746 | 2,328 | 1,91 | 1,492 | 1,074 |
| ei | 0,018 | -0,264 | 0,454 | -0,528 | 0,39 | 0,208 | -0,274 |
| Сумма ei | 0,825 |
Дата добавления: 2020-10-01; просмотров: 621;











