Поиск экстремумов функции

ИССЛЕДОВАНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ

Важным разделом математики является исследование аналитических функций. Оно обычно заключается в определении координат особых точек функции и её значений, а также в выяснении особенностей функции, такие как наличие точек разрыва, асимптот, точек перегибов и.т.д.

С помощью функции fsolve легко находятся значения независимой переменной 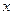функции вида 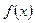, при которых 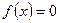(корни уравнения). При этом данная функция позволяет (в отличие от функции solve) изолировать корни функции указанием примерного интервала их существования. Ряд функций служат для вычисления экстремумов, максимумов и минимумов функций, а также для определения их непрерывности.

Поиск экстремумов функции

Библиотечная функция extrema

extrema(expr, constrs)

extrema(expr, constrs, vars)

extrema(expr, constrs, vars, `s`)

позволяет найти экстремумы выражения expr (как максимума, так и минимумы) при ограничениях constrs и переменных vars, по которым ищется экстремум. Ограничения constrs и переменные vars могут задаваться одиночными объектами или списками ряда ограничений и переменных Найденные координаты точек экстремума присваиваются переменной `s`. При отсутствии ограничений в виде равенств или неравенств вместо них записывается пустой список {}.

> readlib(extrema):

> extrema( a*x^2+b*x+c,{},x );

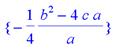
> extrema(2-(2*(x^2+3))/(x^2+2*x+5),{},x);

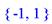
> extrema(2-(2*(x^2+3))/(x^2+2*x+5),{-5,-2.8},x,'s');s;

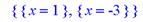
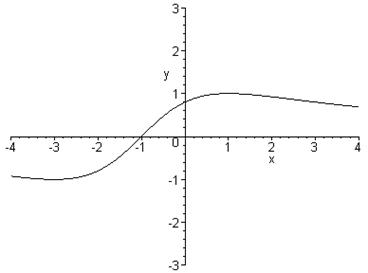
> plot(2-(2*(x^2+3))/(x^2+2*x+5),x=-4..4,y=-3..3,color=black);

> restart;

> R:=2-(2*(x^2+3))/(x^2+2*x+5);

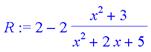
> fsolve(R);

> fsolve(R,x,-3..0);