Определение точек нарушения непрерывности
Очень важно проводить анализ функций на непрерывность. Для этого служит функция discont(f,x), которая позволяет определить точки, в которых нарушается непрерывность функции f(x). Она вычисляет все точки в пределах изменения x. Результаты вычислений могут содержать особые экстрапеременные с именами вида _Zn- и _NNn-. В частности, они позволяют оценить периодические нарушения непрерывности функций.
> discont(arctan(1/2+tan(2*x))/(x^2-1),x);
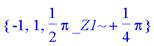
> discont(sin(x)*cos(1/x),x);
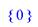
> discont(1/((x-1)*(x+2)),x);
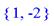
Нахождение сингулярных точек функции
Многие операции, такие как интегрирование и дифференцирование, чувствительны к особенностям функций, в частности к их разрывам и особым точкам. Функции singular(expr,var) позволяет найти особые (сингулярные) точки выражения expr, в которых она испытывает разрывы. Дополнительно в числе параметров может указываться необязательный список переменных.
Примеры применения этой функции приведены ниже:
> readlib(singular):
> singular(ln(x)/(x^2-a));
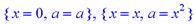
> singular(tan(x));
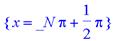
> singular((x+y+1)/x,{x,y});
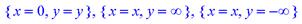
> singular(1/tan(x));
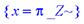
Дата добавления: 2020-10-01; просмотров: 213;











