Подстановки с помощью sub и subsop

Подстановки в общем случае служат для замены одной части выражения на другую. Частными видами подстановок являются такие виды операций, как замена одной переменной на другую или замена символьного значения переменной её численным значением.

Основные операции подстановки выполняют следующие функции.

· subs(x=a,e) – в выражении e заменяет подвыражение x на подвыражение a;

· subs(s1,…,s2,e) – в выражении e заменяет одни подвыражения на другин, выбирая их из списков s1,…,s2 вида x=a;

· subs(eq1,eq2,…,eqn,e) – в выражении e заменяет указанные в eqi операнды другими, указанными в правой части равенств eqi вида ni=ei, где ni – номер операнда, ei – выражение замены.

Все эти функции возвращают изменённое после подстановки выражение. Ниже приведены примеры применения функций подстановок.

> W:=3*x^2+8;

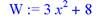
> U:=(2/5)*x^2+3*y;

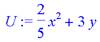
> subs(x=7,y=12,U);

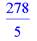
> subs(a=b,b^2-2*a*b-b^2);

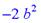
> subs(c=a-b,(a^2-2*a*b+b^2)/c);

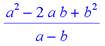
> subsop(1=x,a+b+c);

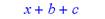
Команда subs с успехом применяется и при подстановке значений переменных в уравнение. Это чрезвычайно важно, например, при проверке корней уравнения. В следующих примерах подставим несколько значений переменной х в уравнение .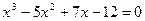

> eqn:=x^3-5*x^2+7*x-12=0;

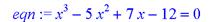
> subs(x=3,eqn);

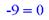
> subs(x=4,eqn);

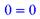
> subs(x=5,eqn);

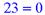
Функции сортировки

Сортировка выражений широко используются в практике символьных преобразований. Для выполнения сортировки служит функция sort, применяемая в одной из следующих форм:

sort(L),sort(L,F), sort(A), sort(A,V),

здесь L – список сортируемых значений, F – необязательная булева процедура с двумя аргументами, A – алгебраическое выражение, V – необязательные дополнительные параметры.

> restart;sort([y,s,f,a,c,i]);

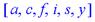
> sort(1+x^2+x);

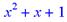
> p:=y^3*x^2+y^2*x*2+x^3+1;

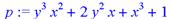
> sort(p,[x,y]);

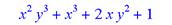
Функции сортировки не работают с символами кирилицы и не позволяют сортировать слова русского языка.