Элементарные логические функции
Основные определения алгебры логики
Алгебра логики– определенная часть математической логики, называемая исчислением высказываний (слайд 2).
Высказывание– утверждение, которое может быть истинным («да») или ложным («нет»). Одно и то же высказывание не может быть одновременно истинным и ложным. Поэтому в алгебре логики рассматриваются только 2 значения высказываний:
· истинное (ему ставится в соответствие значение 1);
· ложное (ему ставится в соответствие значение 0).
Алгебра логики, отвлекаясь от смысловой содержательности высказываний, дает возможность определить, истинны или ложны составные высказывания (функции) алгебраическими методами.
Логические переменные величины и функции от них, которые могут принимать только 2 значения – 0 и 1, называются логическими или булевскими переменными и функциями. Значение логической функции зависит от конкретного сочетания значений всех ее n аргументов - набора аргументов.
Логическая функция от n двоичных аргументов полностью определяется таблицей истинности.Таблица истинности - это таблица, в которую записаны значения логической функции для каждого из 2n наборов аргументов на входе. Для того чтобы полностью определить логическую функцию, достаточно перечислить либо все наборы, при которых эта функция принимает значения, равные 1, либо все наборы, при которых эта функция принимает значения, равные 0.
Элементарные логические функции
Логические функции, зависящие от одной или двух переменных, называются элементарными. К основным логическим функциям относятся следующие элементарные функции: отрицание; логическое умножение; отрицание от логического умножения; логическое сложение; отрицание от логического сложения; равнозначность; отрицание равнозначности.
Функция отрицания - это логическая функция от одного аргумента, которая принимает значение 1, если аргумент равен 0, и принимает значение 0, если аргумент равен 1, и называется отрицанием(инверсией) или логической функцией НЕ (слайд 3).
Запись логической функции НЕ – 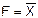 ,где черта над переменной – признак инверсии. Логическая функция НЕ от одного аргумента описывается следующей таблицей истинности:
,где черта над переменной – признак инверсии. Логическая функция НЕ от одного аргумента описывается следующей таблицей истинности:
| X | F |
Функцией логического умноженияn аргументов называется логическая функция, которая принимает значение 1 только в том случае, когда все аргументы равны 1, а 0– во всех остальных случаях (слайд 4).
Функцию логического умножения называют также конъюнкцией или функцией И.
Элементарная функция логического умножения зависит от двух аргументов и описывается следующей таблицей истинности:
| X | Y | F |
Запись логической функции И: F=XΛY ; F=X&Y ; F=X×Y,
где знаки «Λ», «&», «.» – знаки, обозначающие операцию логического умножения. Все варианты записи равнозначны.
Функцией логического сложенияnаргументов называется логическая функция, которая принимает значение 0только в том случае, когда все аргументы равны 0 (т.е. при наборе n нулей), и 1 во всех остальных случаях (т.е. когда хотя бы один аргумент равен 1) (слайд 5).
Функцию логического сложения называют такжедизъюнкциейили логической функцией ИЛИ.
Элементарная дизъюнкция зависит от двух аргументов и описывается следующей таблицей истинности:
| X | Y | F |
Запись логической функции ИЛИ: F=XVY ; F=X+Y, где знаки «V», «+» обозначают операцию логического сложения.
Функция отрицания от логического умножения принимает значение 0, когда все аргументы равны 1, и 1 – во всех остальных случаях (слайд 6):
| X | Y | F |
Запись логической функции: 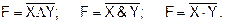
Функция отрицания от логического сложения принимает значение 1, когда все аргументы равны 0, и значение 0 – во всех остальных случаях (слайд 7):
| X | Y | F |
Запись логической функции: 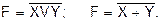
В сложных выражениях с использованием логических операций И, ИЛИ, НЕ сначала выполняются операции отрицания НЕ, затем операции конъюнкции И и, в последнюю очередь, операции дизъюнкции ИЛИ.
Для того, чтобы изменить указанную последовательность выполнения операций, в выражениях следует использовать скобки.
Например: 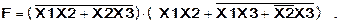
Дата добавления: 2020-10-01; просмотров: 1487;











