Правила упрощения логических функций

Пусть дана некоторая логическая функция либо в аналитическом виде, либо в виде таблицы, в которой перечислены значения функции при всех возможных наборах аргументов (слайды 21-23).

Требуется определить вид простейшей формулы, выражающей заданную функцию, которая содержит минимальное количество элементарных логических функций И, ИЛИ, НЕ.

Эта простейшая формула может иметь

а) либо нормальную дизъюнктивную форму;

б) либо нормальную конъюнктивную форму;

в) либо какой-нибудь еще тип.

Нахождение такой простейшей формулы, выражающей заданную функцию, удобно выполнять в несколько этапов.

На первом этапе логическая функция представляется в СДНФ или в СКНФ.

Если исходная функция задана таблицей, и количество наборов аргументов, при которых функция равна 1, меньше количества наборов, при которых она равна 0, то наиболее простой окажется СДНФ, в противном случае - СКНФ.

Если исходная функция задана аналитически, то преобразование ее в СДНФ или СКНФ выполняется в такой последовательности:

1) Путем последовательного применения законов инверсии, логическая функция приводится к нормальной форме, в которой инверсия применяется только к аргументам, но не к функциям от них.

2) Путем раскрытия скобок (по известным формулам) логическая функция приводится к дизъюнктивной нормальной или конъюнктивной нормальной форме (где ДНФ- дизъюнкция ряда членов, которые есть конъюнкция аргументов, взятых с инверсией или без нее; а КНФ- конъюнкция ряда членов, которые есть дизъюнкция аргументов, взятых с инверсией или без нее.)

3) Если это ДНФ, и каждый член представляет собой конъюнкцию менее n членов, (n - количество аргументов функции), то каждый такой член умножается на выражение 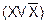, тождественно равное 1 (Х - один из аргументов, которые в данной дизъюнкции отсутствуют). В результате чего конъюнкция превращается в дизъюнкцию двух конъюнкций (расширение ДНФ):

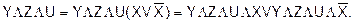
Если же это КНФ, то к каждому члену, представляющему собой дизъюнкцию менее n членов (n - количество аргументов), добавляется член 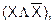тождественно равный 0 (Х - аргумент, отсутствующий в данной дизъюнкции). В результате чего каждый из этих членов превращается в конъюнкцию двух дизъюнкций (расширение КНФ):

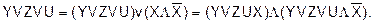
4)Приводятся подобные члены (исключаются одинаковые слагаемые ДНФ или сомножители КНФ).

Далее п.п. 3-4 повторяются до тех пор, пока функция не будет представлена в СДНФ или СКНФ, т.е. количество членов в каждой конъюнкции (дизъюнкции) не станет равным n и не станет совпадающих дизъюнкций (конъюнкций).

На втором этапе происходит преобразование (минимизация) полученной логической функции по известным правилам, приведенным выше.