МЕТОДЫ РАСЧЕТА СРЕДНЕЭФФЕКТИВНОЙ ДОЗЫ

ТОКСИКАНТОВ

Среднесмертельную дозу вычисляют статистическими метода­ми. Наиболее известны методы Беренса, Кербера, Першина, Бе-ренса и Шлоссера, метод наименьших квадратов, методы пробит-анализа Миллера и Тейтнера, Лигчфилда и Уилкоксона, метод Штабского и некоторые другие.

При выявлении эффективной дозы какого-либо вещества, вы­зывающего конкретный эффект, находят не одно определенное значение, а ряд значений, которые образуют вариационный ряд его индивидуальных эффективных доз. Распределение частот ин­дивидуальных эффективных доз в этом вариационном ряду обыч­но приближается к нормальному распределению.

В условиях нормального распределения вариационный ряд мо­жет быть полностью определен средней арифметической варьиру­ющего признака (в данном случае — доза) и величиной стандар­тного отклонения (σ), соответствующего стандартной ошибке средней арифметической (σ) из индивидуальных минимальных эффективных доз. Найти ее можно, используя известную фор­мулу:

σ = 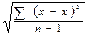где х — значение отдельного наблюдения; х—средняя арифметическая вариаци­онного ряда; л —число наблюдений.

Другой путь определения средней эффективной дозы вытекает из особенностей кривой нормального распределения. Площадь над осью абсцисс, ограниченная этой кривой, выражает общее количество животных, у которых наблюдалась изучаемая реакция (рис. 2.1, Л).

Так как кривая нормального распределения симметрична, тс перпендикуляр, восстановленный из точки , соответствующей средней эффективной дозе, разделит всю площадь, ограниченную кривой, на две равные части. Следовательно, средняя эффектив­ная доза вместе с тем является той дозой, которая вызывает изуча­емый эффект у 50 % подопытных животных.

Итак, вместо того, чтобы на очень большом количестве живот­ных определять эффективные дозы и из них вычислять среднюю арифметическую, можно избрать более простой путь — искать ту дозу, которая вызывает изучаемый эффект у 50 % подопытных жи­вотных.

Если изучать на животных действие последовательно возраста­ющих доз исследуемого вещества, разделив для этого животных на ряд групп и испытывая на каждой группе какую-либо одну дозу, то окажется, что учитываемая реакция проявляется лишь начиная с какой-то определенной дозы, частота возникновения этой реак­ции будет нарастать и, наконец, при какой-то величине дозы эта реакция наступит у всех животных данной группы. Зависимость между величиной дозы и частотой возникновения реакции можно изобразить графически. Для этого по оси абсцисс следует отло­жить дозы, а по оси ординат — частоту возникновения учитывае­мого эффекта к числу животных, на которых данную дозу испыта­ли (см. рис. 2.1, Б). При этом зависимость между дозой и частотой наступления реакции будет представлена симметричной S-образной кривой, которую обычно называют кумулятой или характери­стической кривой. На этой кривой средняя эффективная доза со­ответствует значению абсциссы для той части кривой, ордината которой равна 50 %.

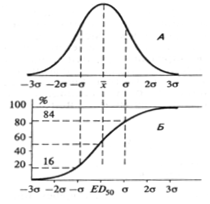
Рис. 2.1. Соотношение между кривой нормального распределения (А) и соответствуюшей ей кумулятой (Б)

Для стандартизированной кривой нормального распределения, т. е. при стандартном отклонении теоретического распределения при о= 1, следует отметить, что при σ = - 1 площадь, отсекаемая перпендикуляром, восстановленным из этой точки, составляет 16 % (точнее, 15,87 %) общей площади, ограниченной кривой рас­пределения; при σ = +1 отсекаемая площадь составляет 84 % (точ­нее, 84,13%) общей площади, ограниченной кривой распределе­ния. Следовательно, доза вещества, которая меньше, чем LD₅₀, на величину стандарта, должна вызывать реакцию у 16% животных, доза, превышающая LD₅₀ на величину стандарта, должна вызывать реакцию у 84 % животных. Эти дозы соответственно обозначают LD ₁₆ и LD₈₄.

Итак, LD₁₆ = LI₅₀- σ; LD₈₄ = LD₅₀ + σ

Отсюда: LD₈₄ — LD₁₆ = LD₅₀ + σ - LD₅₀+ σ = 2 σ, следовательно,

σ = ( LD₈₄ — LD₁₆ )/2.

Это соотношение часто используется для нахождения стандар­тного отклонения и стандартной ошибки LD_50.

Характеристическая кривая имеет исключительно большое значение для количественной оценки фармакологической актив­ности. По существу, все методы количественного определения активности сводятся к построению характеристической кривой или эквивалентной ей прямой на основании данных, получен­ных в результате эксперимента, и к последующему их анализу.

МЕТОД БЕРЕНСА

Метод вычисления LD₅₀ по Беренсу основывается на том поло­жении, что общее количество животных, погибших от доз, мень­ших LD₅₀, равно общему количеству животных, выживших от доз, больших LD₅₀). Для обработки экспериментального материала по методу Беренса необходимо, чтобы интервал между испытывае­мыми дозами был одинаков и чтобы для испытания каждой из доз было использовано одинаковое количество животных. Для вырав­нивания экспериментальной характеристической кривой Беренс предложил прием так называемого накопления частот. Этот при­ем заключается в том, что к числу животных, погибших от каждой из испытанных доз, прибавляется количество животных, погиб­ших от всех меньших испытанных доз, а к числу животных, вы­живших от каждой из испытанных доз, прибавляют количество животных, выживших от всех более высоких испытанных доз.

Логически этот прием вполне оправдан. Так, если данное жи­вотное погибло под влиянием какой-то дозы изучаемого вещества, то оно, несомненно, погибло бы, если бы это вещество было введено в более высокой дозе; наоборот, если данное животное осталось в живых после введения ему определенной дозы изучае­мого вещества, то оно, бесспорно, выжило бы, если бы это веще­ство было ему введено в меньшей дозе.

На основании вычисленных накопленных частот подсчитыва­ют смертность от каждой из испытанных доз в процентах и строят характеристическую кривую, откладывая по оси абсцисс испытан­ные дозы, а по оси ординат — проценты смертельных исходов. Ве­личина LD₅₀ может быть найдена непосредственно из графика. Для этого из той точки характеристической кривой, которой соот­ветствует 50 % смертельных исходов, опускают перпендикуляр на ось абсцисс; величине LD₅₀ соответствует точка пересечения этого перпендикуляра с осью абсцисс.

Близкую по значению величину LD₅₀ можно получить и без по­строения графика. Так как в средней части характеристической кривой небольшой ее отрезок мало отличается от прямой линии, то величину LD₅₀ можно вычислить путем прямолинейного интер­полирования между ближайшими к LD₅₀ меньшей и большей до­зами.

Если интервал между испытанными дозами равен d, а величина LD₅₀ находится между А и В, из которых доза А вызвала а % смер­тельных исходов (а<50) и доза В—Ь% смертельных исходов

(b>50), LD₅₀ = .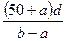

Практическое использование метода Беренса можно проиллю­стрировать на примере обработки экспериментального материа­ла по изучению токсичности тубазида, подробно описанного М. Л. Беленьким (1963).

Процесс обработки представлен в таблице 2.1.