Лекция 8. Синтез нерекурсивных цифровых фильтров
8.1. Классификация нерекурсивных цифровых фильтров
К нерекурсивным цифровым фильтрам можно отнести:
- фильтры с линейной ФЧХ;
- частотно-селективные фильтры;
- цифровые преобразователи Гильберта (ЦПГ);
- цифровые дифференциаторы (ЦД);
- согласованные фильтры.
8.2. Синтез нерекурсивных фильтров методом окон
Для данного метода задается желаемый коэффициент передачи в виде непрерывной периодической функции, определенной в диапазоне частот от нуля до частоты Найквиста 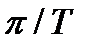 .
.
Непрерывная периодическая функция может быть разложена в ряд по отсчетам импульсной характеристики:
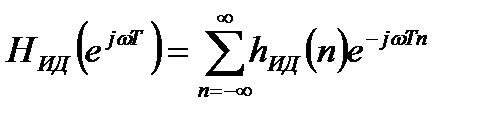 . (8.1)
. (8.1)
Рисунок 8.1 – идеальная АЧХ ПФ
Для получения бесконечной последовательности отсчетов идеальной импульсной характеристики вычисляется обратное преобразование Фурье:
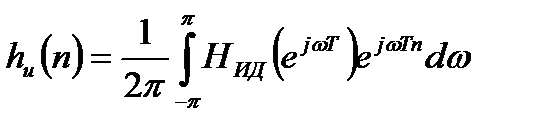 . (8.2)
. (8.2)
Рисунок 8.2 – процедура усечения импульсной характеристики
Для получения реализуемого нерекурсивного фильтра заданного порядка бесконечная последовательность импульсной характеристики усекается. В результате усечения получается частотная характеристика синтезированного фильтра:
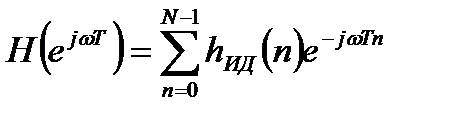 . (8.3)
. (8.3)
После замены 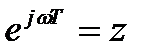 получим передаточную функцию цифрового фильтра:
получим передаточную функцию цифрового фильтра:
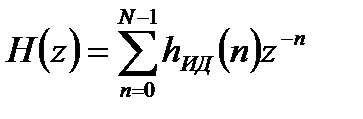 . (8.4)
. (8.4)
Рисунок 8.3 – искажения частотной характеристики
Из-за усечения появляются:
- переходные полосы между областями пропускания и задерживания;
- пульсации 9% на границах полос пропускания и задерживания (явление Гиббса);
- колебания коэффициента передачи в полосе пропускания;
- в полосах задерживания АЧХ принимает лепестковый характер и не равна нулю.
Для ослабления указанных эффектов и в первую очередь для уменьшения уровня лепестков в полосах задержания усеченная импульсная характеристика умножается на весовую функцию, плавно спадающую к краям:
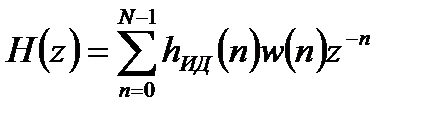 . (8.5)
. (8.5)
Платой за уменьшение уровня боковых лепестков является некоторое расширение полосы пропускания.
| Тип окна | Уровень боковых лепестков, дБ |
| прямоугольное | -13.0 |
| Треугольное (Бартлетта) | -26.5 |
| Ханна | -44.0 |
| Хэмминга | -53.6 |
| Блэкмена | -75.3 |
| Кайзера при β=4 | -45.2 |
| Кайзера при β=9 | -90.5 |
| Чебышева при β=40 дБ | -51.0 |
| Чебышева при β=60 дБ | -71.6 |
| Чебышева при β=80 дБ | -92.4 |
8.3. Схемы и характеристики нерекурсивных фильтров с линейной ФЧХ
ЦФ фильтры с линейной ФЧХ позволяют передавать сигналы без искажения их формы.
Линейность ФЧХ нерекурсивных фильтров обеспечивается при выполнении единственного условия: симметрии или антисимметрии импульсной характеристики:
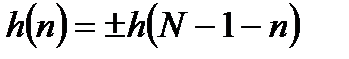 , (8.6)
, (8.6)
где 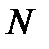 - полное число отсчетов импульсной характеристики, включая нулевой.
- полное число отсчетов импульсной характеристики, включая нулевой.
Нерекурсивные цифровые фильтры с линейной ФЧХ отличаются своими характеристиками в зависимости:
- от симметричности или антисимметричности;
- от четности или нечетности числа отсчетов.
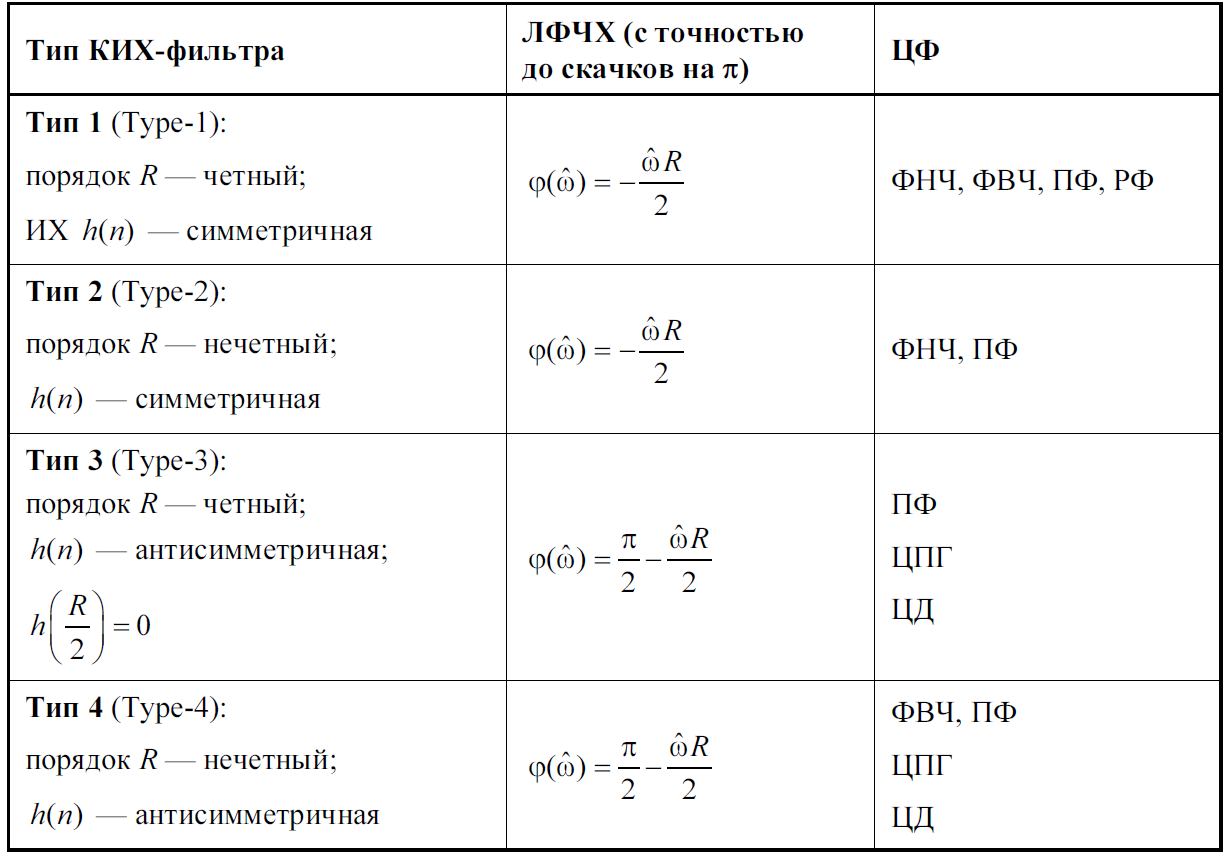
Соответственно, существуют четыре типа нерекурсивных фильтров с линейными ФЧХ.
Симметричные фильтры с четным числом отсчетов N
Импульсная характеристика таких фильтров определяется выражением:
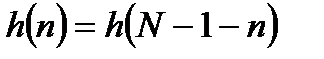 . (3.2)
. (3.2)
Передаточная характеристика такого фильтра с учетом свойства симметрии описывается выражением:
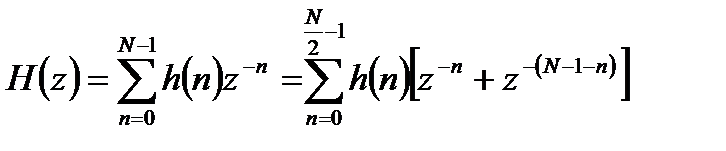 . (3.3)
. (3.3)
После преобразований можно получить выражение для частотной характеристики:
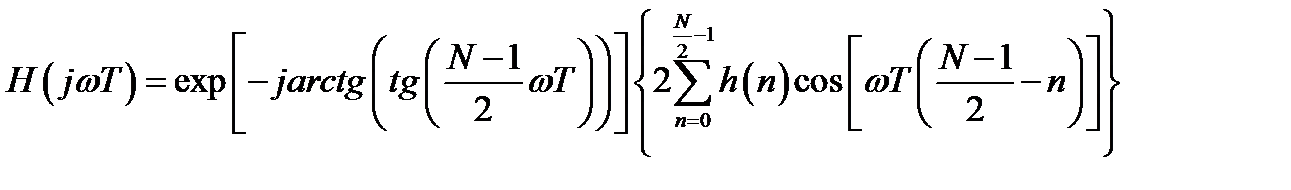 . (3.3)
. (3.3)
Соответственно, вещественная частотная характеристика (ВЧХ) и ФЧХ фильтра имеют вид:
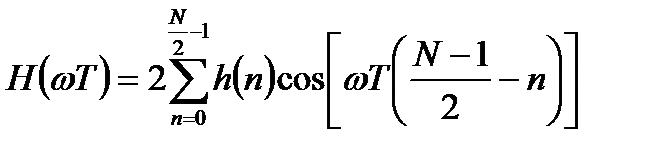 ; (3.4)
; (3.4)
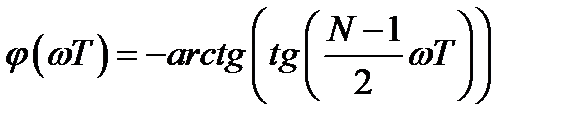 . (3.5)
. (3.5)
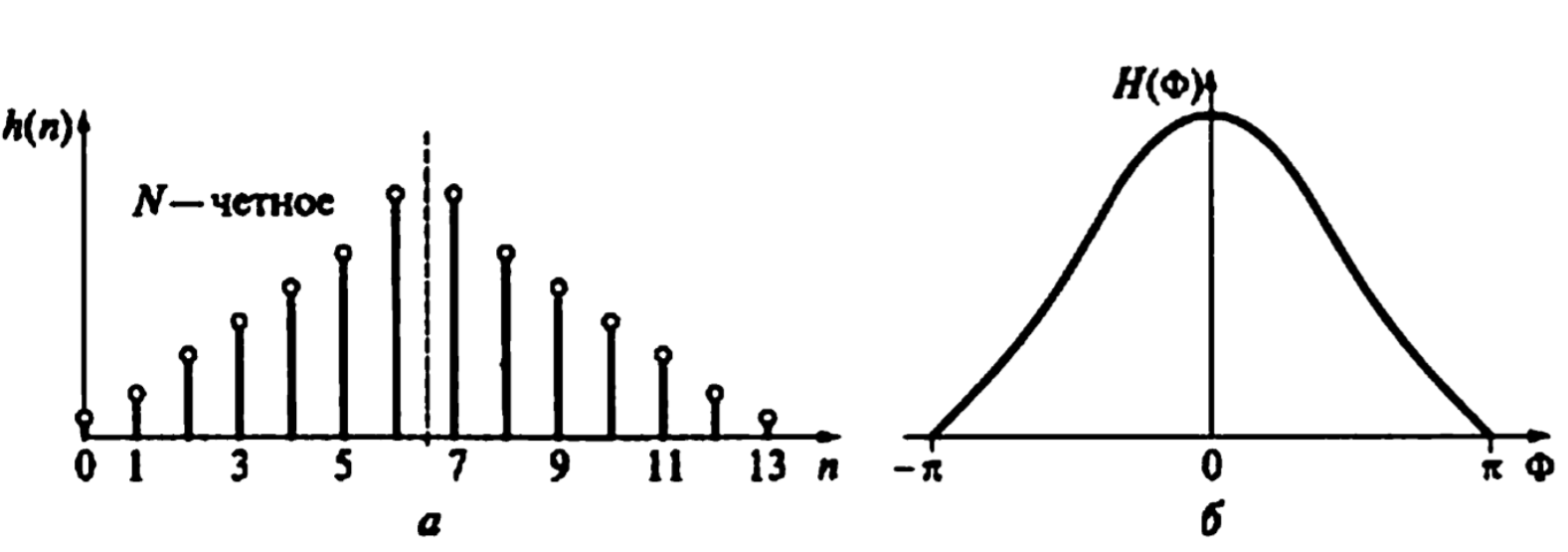
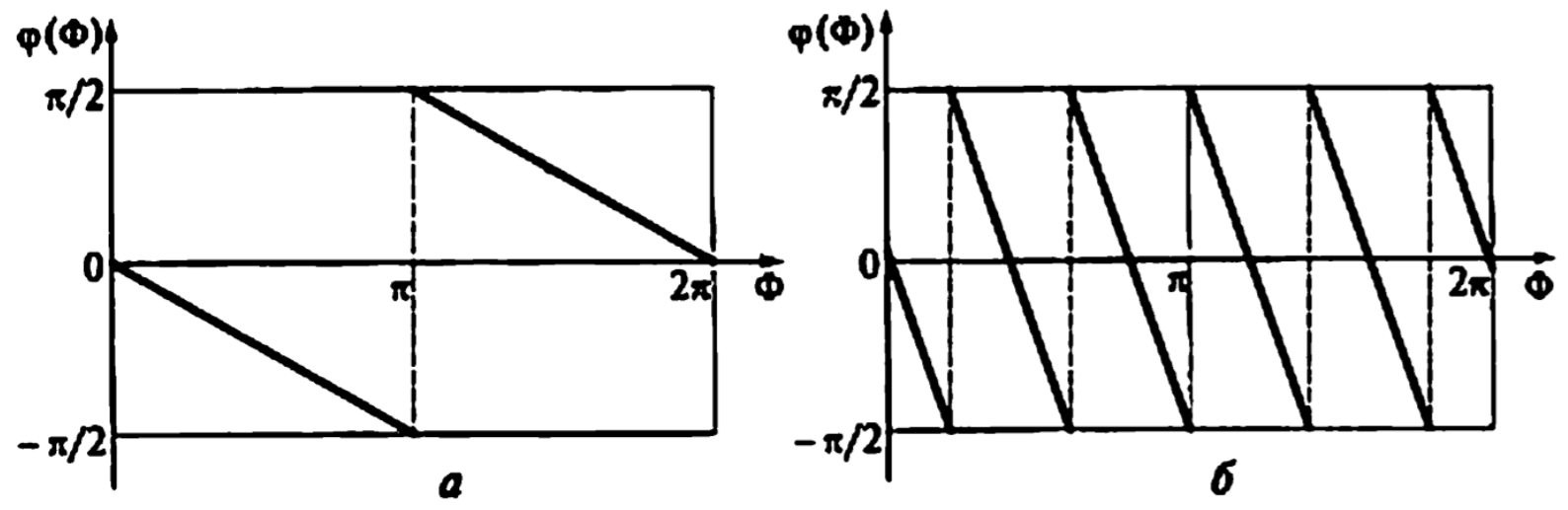
Рисунок 3.1 – характеристики рекурсивного фильтра типа 1 (a - N=2, б - N=6)
ВЧХ является четной функцией аргумента 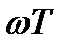 .
.
На частоте Найквиста 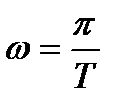 , ЧХ всегда равна нулю.
, ЧХ всегда равна нулю.
ФЧХ является линейно-разрывной функцией.
ФЧХ антисимметрична относительно частоты Найквиста:
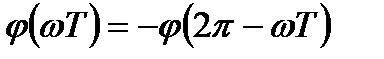 . (3.6)
. (3.6)
Возможно реализовывать только ФНЧ и ПФ. Невозможно реализовывать ФВЧ и РФ.
Антисимметричные фильтры с четным числом отсчетов N
Импульсная характеристика таких фильтров определяется выражением:
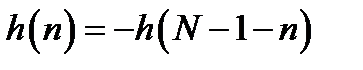 . (3.7)
. (3.7)
Выражение для частотной характеристики такого фильтра может быть получено в виде:
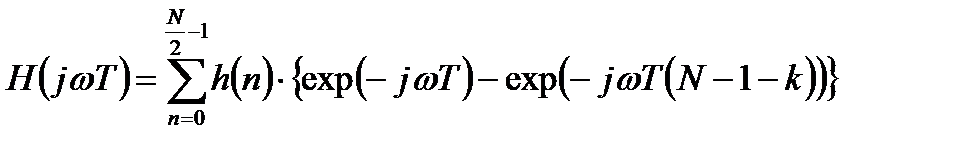 . (3.8)
. (3.8)
Соответственно, вещественная частотная характеристика (ВЧХ) и ФЧХ фильтра имеют вид:
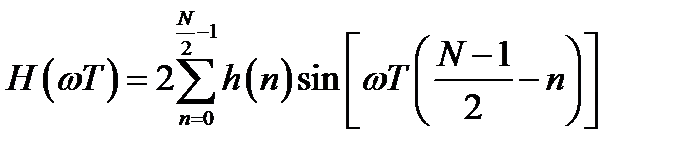 ; (3.9)
; (3.9)
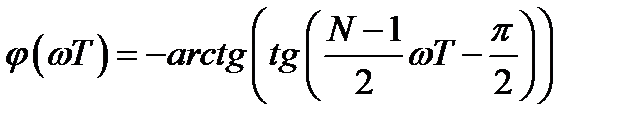 . (3.10)
. (3.10)
ВЧХ является нечетной функцией аргумента 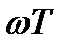 .
.
На нулевой частоте ЧХ равна нулю.
ФЧХ является линейно-разрывной функцией, антисимметрична относительно частоты Найквиста:
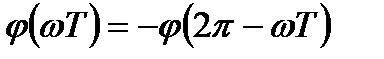 . (3.11)
. (3.11)
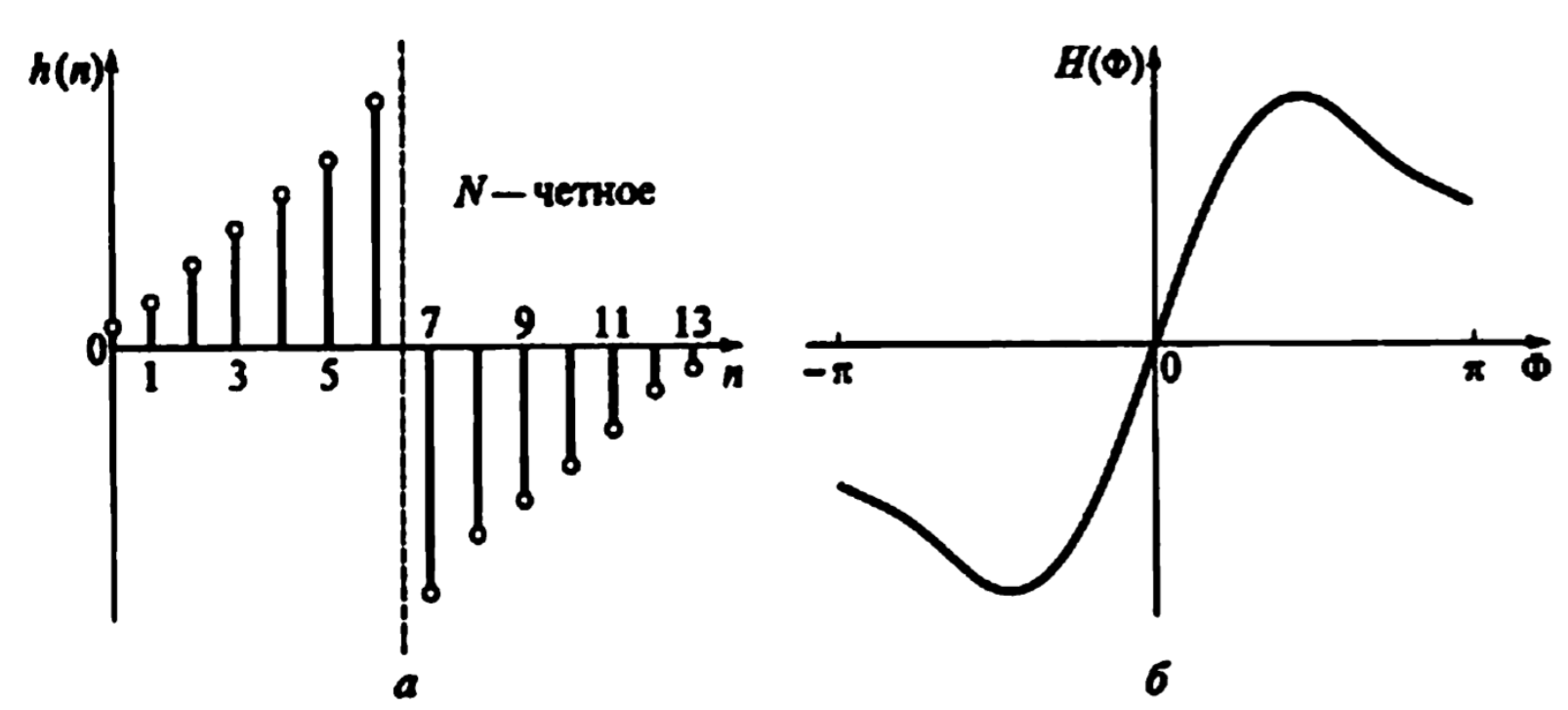
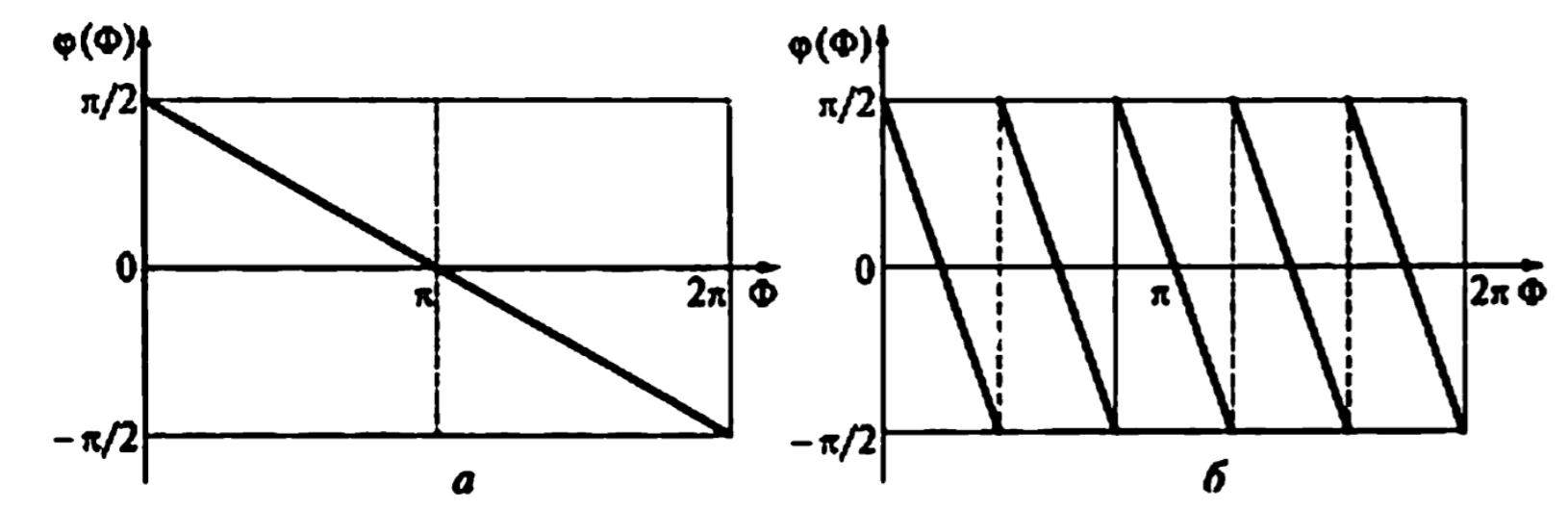
Рисунок 3.2 – характеристики рекурсивного фильтра типа 2 (a - N=2, б - N=6)
Возможна реализация фильтров ФВЧ и ПФ, ЦПГ, ЦД.
Фильтр непригоден для проектирования ФНЧ.
Симметричные фильтры с нечетным N
Импульсная характеристика таких фильтров определяется выражением:
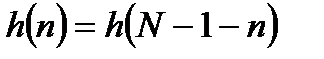 . (3.12)
. (3.12)
Вещественная ЧХ фильтра имеет вид:
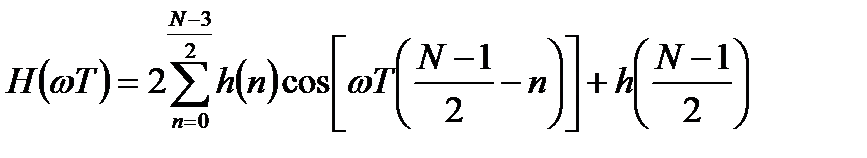 . (3.13)
. (3.13)
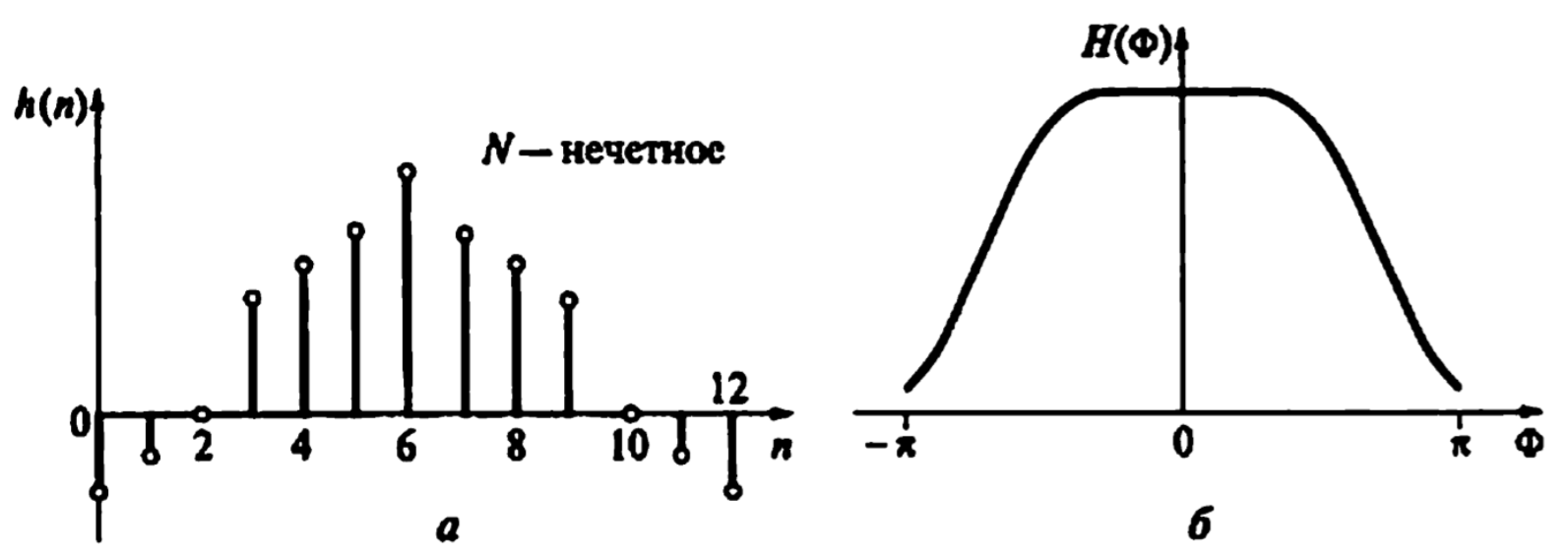
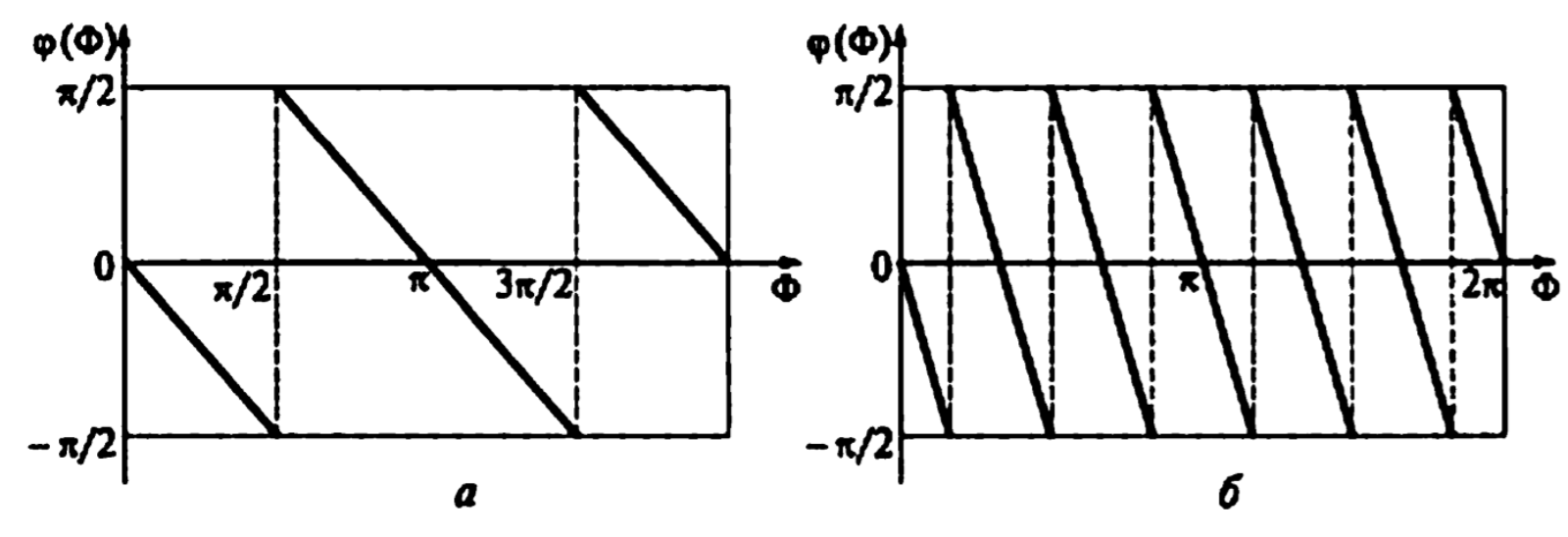
Рисунок 3.3 – характеристики рекурсивного фильтра типа 3 (a - N=3, б - N=7)
ЧХ является четной функцией частоты. ЧХ не равна нулю на частоте Найквиста.
Такие фильтры могут реализовывать произвольную избирательности (ФНЧ, ФВЧ, ПФ, РФ и др.).
Антисимметричные фильтры с нечетным N
Импульсная характеристика таких фильтров определяется выражением:
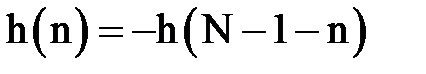 . (3.14)
. (3.14)
ЧХ фильтра имеет вид:
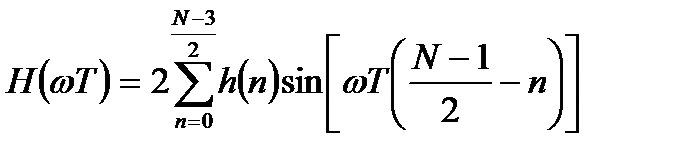 . (3.15)
. (3.15)
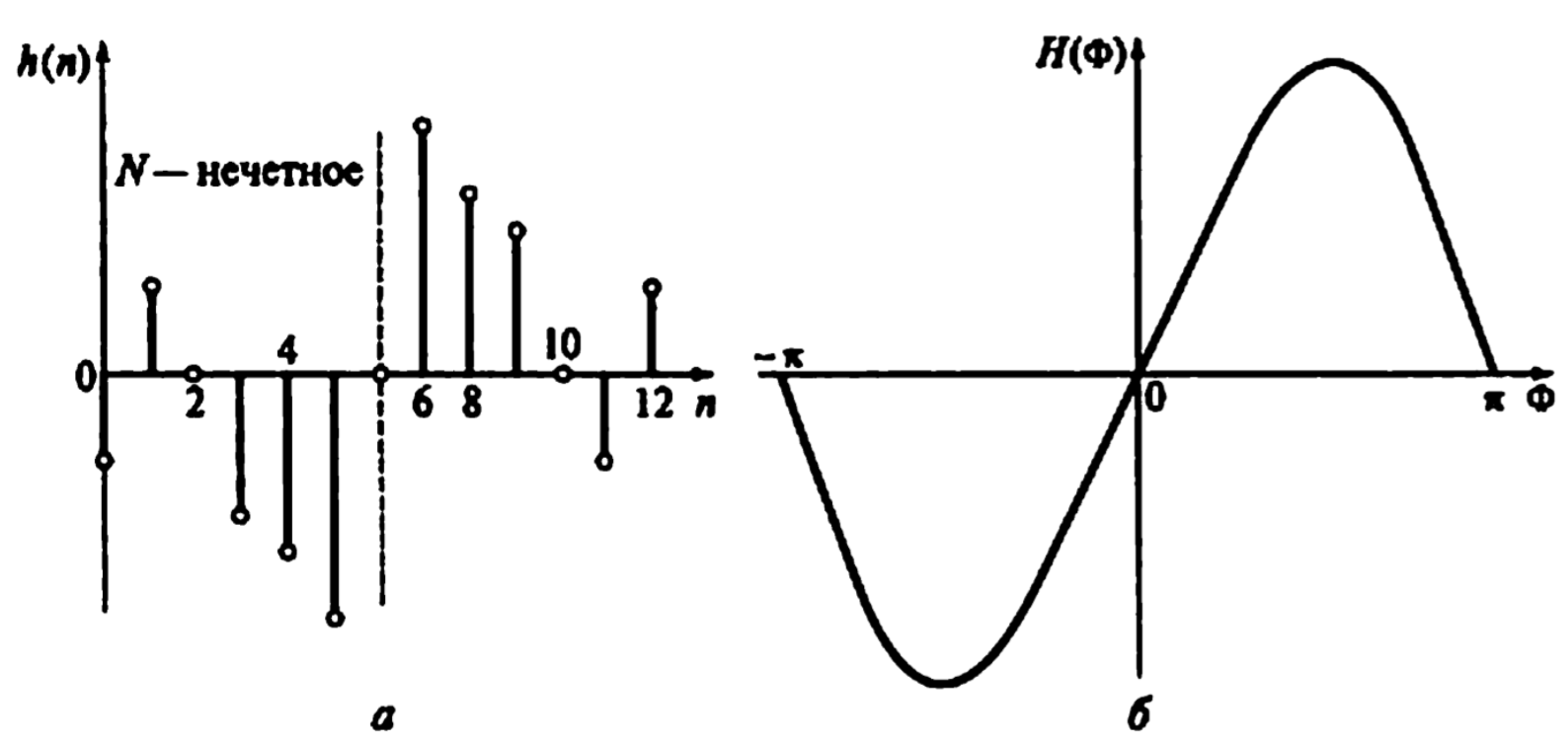
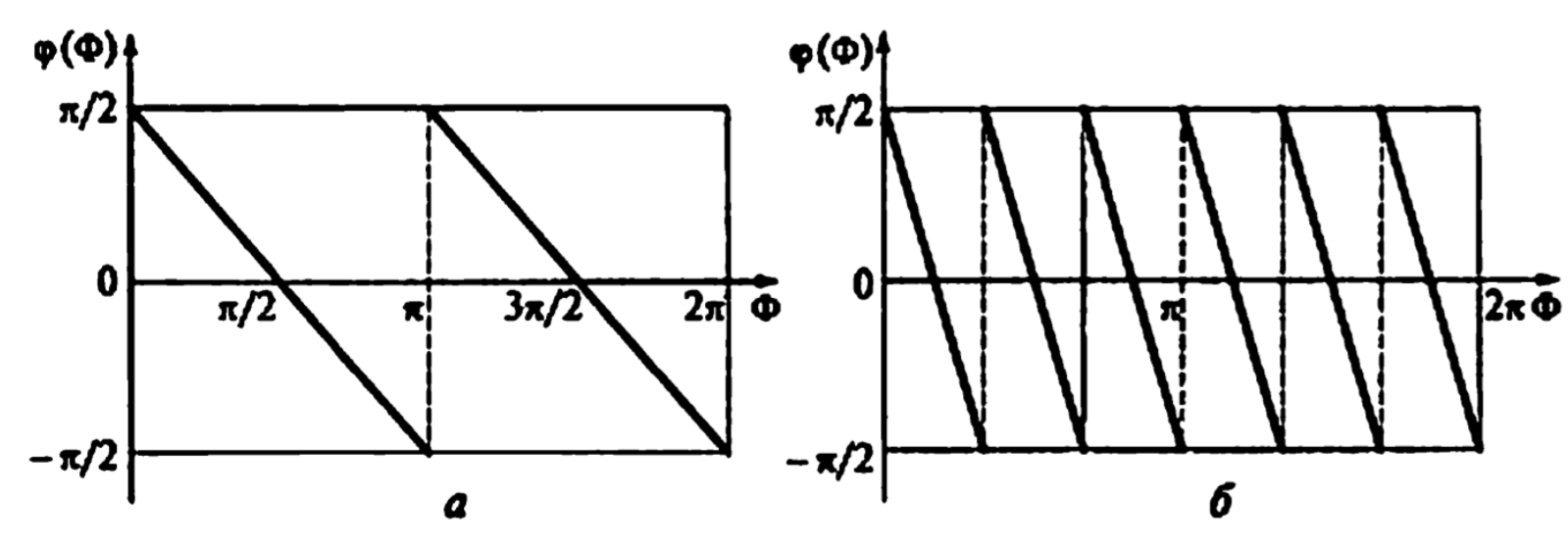
Рисунок 3.4 – характеристики рекурсивного фильтра типа 4 (a - N=3, б - N=7)
ЧХ является нечетной функцией частоты. ЧХ равна нулю как при нулевом значении частоты, так и на частоте Найквиста.
Такой фильтр целесообразно использовать только при проектировании полосового фильтра.
Литература
Маркович И.И. Цифровая обработка сигналов в системах и устройствах: монография / И.И. Маркович; Южный федеральный университет. – Ростов н/Д: Издательство Южного федерального университета, 2012. – 236 с. (стр. 108)
Гадзиковский В.И. Цифровая обработка сигналов. М.: СОЛОН-ПРЕСС, 2013. – 766 с. (с. 102)
Солонина А.И., Арбузов С.М. Цифровая обработка сигналов. Моделирование в MATLAB / А.И. Солонина, С.М. Арбузов. – СПб.: БХВ – Петербург, 2008. 816 с.
Васильев В.П. Основы теории и расчета цифровых фильтров: учеб. Пособие / В.П. Васильев, Э.Л. Муро, 2-е изд., стереотип. – М.: ИНФРА – М, 2018. – 272 с.
Варгаузин В.А. Цифровая обработка сигналов: Минимаксные аппроксимации для задач цифровой фильтрации: Учеб. пособие. СПб.: Изд-во СПбГПУ, 2004. – 87 с.
Дата добавления: 2020-08-31; просмотров: 873;











