Структурные схемы ЛДС
ЛДС могут быть реализованы способами:
- аппаратным;
- программным.
В первом случае используются микросхемы в виде регистров, умножителей, сумматоров. Во втором случае составляется программа расчета с указанием, какие операции и в какой последовательности необходимо выполнить.
Для одной и той же передаточной функции ЛДС может быть реализована различными структурными схемами при аппаратной реализации и различными алгоритмамипри программной реализации.
Различные варианты реализации могут отличаться:
- разной степенью чувствительности к ошибкам ограниченной разрядности;
- различной сложностью реализации (число регистров и сумматоров);
- возможностью распараллеливания вычислений.
Сложность реализации некоторых вариантов структурных схем ЛДС отображена в Таблице 6.1.
Таблица 6.1. Сложность структурной реализации ЛДС
| Прямая форма | Обращенная форма | Каноническая форма 1 | Каноническая форма 2 | |
| Элементы задержки | 2N | 2N | N | N |
| Число умножений | 2N+1 | 2N+1 | 2N+1 | 2N+1 |
| Сумматоры | 2N | N+1 | ||
| Число точек распределения сигналов | 2N | N+1 |
6.3.1. Прямая и обращенная структуры ЛДС
Прямая структура основана на представлении передаточной функции ЛДС в общем виде:
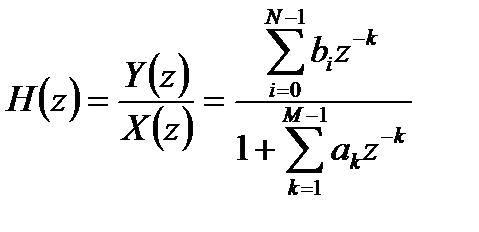 . (6.11)
. (6.11)
Такой передаточной функции соответствует уравнение фильтрации вида:
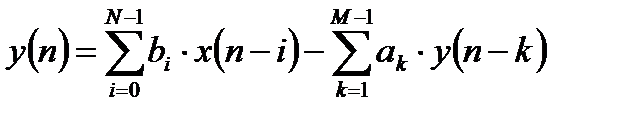 . (6.12)
. (6.12)
Прямая структура ЛДС 2-го порядка имеет вид, приведенный на рисунке 6.1.
Рисунок 6.1 – прямая структура рекурсивного фильтра 2-го порядка
Выходом ЛДС с прямой структурой является выход сумматора. В схеме четко выделены нерекурсивная и рекурсивная части. В прямой структуре в линиях задержки хранятся непосредственно отсчеты входного и выходного сигналов. Повышенная разрядность линий задержки не требуется. Однако в прямой структуре необходим сумматор повышенной разрядности.
Обращенная структура
Обращенная структура соответствует последовательному включению рекурсивной и нерекурсивной части. Один из вариантов обращенных структур характеризуется использованием двухвходовых сумматоров и описывается алгоритмами:
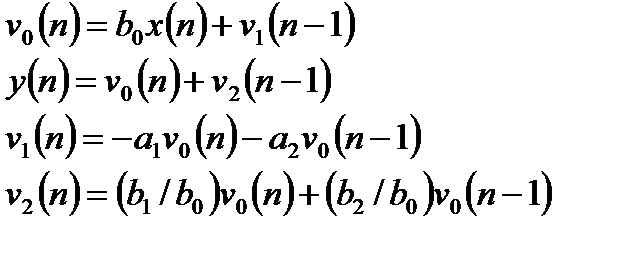 . (6.13)
. (6.13)
Рисунок 6.2 – обращенная структура рекурсивного фильтра 2-го порядка
6.3.2. Канонические структуры ЛДС
Структуру ЛДС называют канонической, если число элементов задержки минимально и равно порядку передаточной функции.
Известно более 30 канонических структур ЛДС второго порядка, среди которых практическое применение нашли 2 структуры, характеризуемые минимальным количеством умножителей.
Каноническая структура 1
Эта структура основана на эквивалентном представлении передаточной функции в виде произведения:
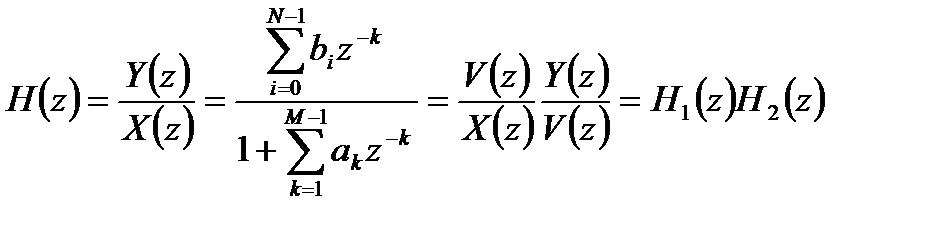 , (6.14)
, (6.14)
где 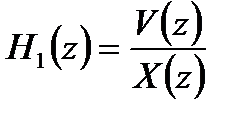 ;
;
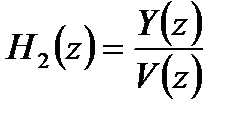 .
.
Алгоритмы работы канонической структуры 1 для 2-ого порядка имеют вид:
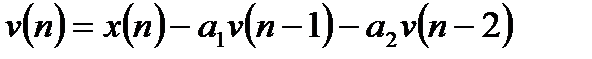 , (6.19)
, (6.19)
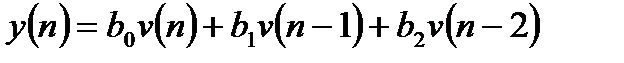 . (6.20)
. (6.20)
Данные прямые структуры для ЛДС 2-ого порядка показаны на рисунке 6.3. Объединение двух линий задержки в одну приводит к прямой канонической структуре 1, изображенной на рисунке 6.3.
Рисунок 6.3 – каноническая структура 1 рекурсивной ЛДС 2-го порядка
Для канонической структуры 1 отсчеты сигналов в линиях задержки могут существенно превосходить по амплитуде входной и выходной сигналы, что требует увеличения разрядности представления чисел в линиях задержки.
Каноническая структура 2
Алгоритмы работы канонической структуры 2 записываются следующим образом:
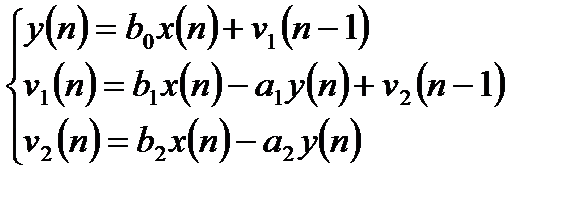 . (6.25)
. (6.25)
Каноническая структура 2 также называется транспонированной формой. Транспонированная форма позволяет эффективно распараллелить вычисления и применяется при аппаратной реализации в специализированных интегральных схемах и ПЛИС.
Рисунок 6.4 – каноническая структура 2
6.3.3. Последовательная и параллельная структуры ЛДС
ЛДС высокого порядка никогда не реализуются в прямой или канонической форме полного порядка. Эффекты конечной разрядности меньше влияют на характеристики ЛДС, если их представить в виде последовательной или параллельной структуры, содержащей ЛДС второго порядка.
Последовательная (каскадная) форма ЛДС основана на представлении передаточной функции через произведение простейших сомножителей второго порядка:
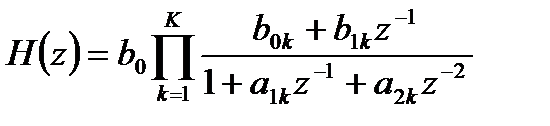 , (6.26)
, (6.26)
где 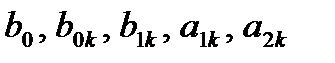 - вещественные коэффициенты;
- вещественные коэффициенты;
K – количество звеньев.
Параллельная форма ЛДС основана на представлении передаточной функции в виде суммы простых дробей второй степени:
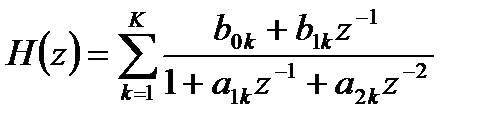 , (6.27)
, (6.27)
где 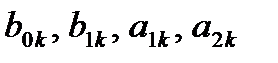 - вещественные коэффициенты;
- вещественные коэффициенты;
K – количество звеньев.
Литература
Петровский А.А. Методы и микропроцессорные средства обработки широкополосных и быстропротекающих процессов в реальном времени / Под ред. Г.В. Римского. – Мн.: Наука и техника, 1988. – 272 с.
Дата добавления: 2020-08-31; просмотров: 895;











