Рекурсивные и нерекурсивные ЛДС

ЛДС называется рекурсивной, если хотя бы один из коэффициентов 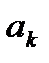разностного уравнения не равен нулю:

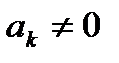, хотя бы для одного из значений 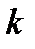. (6.1)

Согласно разностному уравнению, реакция 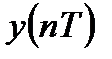рекурсивной ЛДС в каждый момент времени 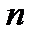определяется:

- текущим отсчетом входного сигнала;

- предысторией входного сигнала;

- предысторией выходного сигнала.

Так как при вычислении выходного сигнала используются предыдущие отсчеты выходного сигнала, то в схеме вычислений присутствуют обратные связи. Поэтому такие фильтры называются рекурсивными (recursive).

Разностное уравнение рекурсивной ЛДС второго порядка имеет вид:

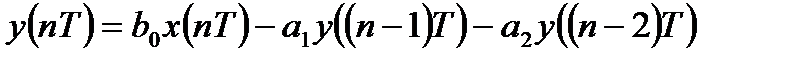. (6.3)

ЛДС называется нерекурсивной, если все коэффициенты 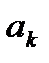разностного уравнения равны нулю:

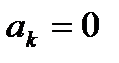. (6.4)

Для нерекурсивной ЛДС разностное уравнение принимает вид:

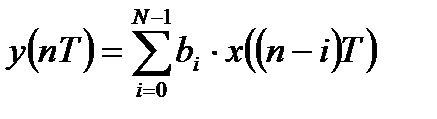. (6.5)

Реакция 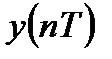нерекурсивной ЛДС определяется:

- текущим отсчетом входного сигнала;

- предысторией входного сигнала.

Из-за отсутствия обратных связей такие фильтры называются нерекурсивными. Иногда применяется термин «трансверсальный фильтр».

Разностное уравнение нерекурсивной ЛДС второго порядка имеет вид:

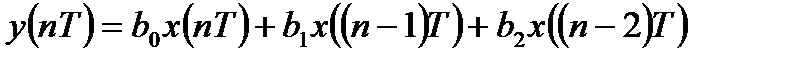. (6.6)