Описание линейной дискретной системы в Z – области

Передаточная функция ЛДС

Передаточная функция - это отношение z – преобразования выходного сигнала 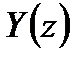к z – преобразованию входного сигнала :

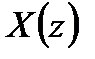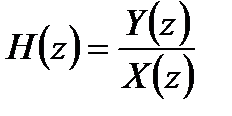. (5.9)

Применим z – преобразование к уравнению линейной свертки 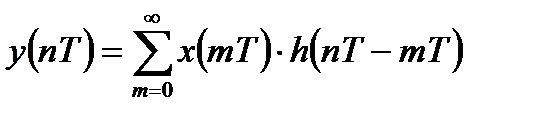. В соответствии со свойствами z – преобразования получим:

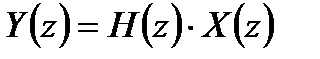, (5.10)

где 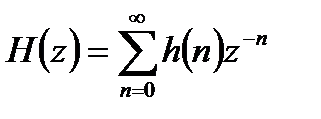- z – преобразование импульсной характеристики.

Таким образом, z – преобразование импульсной характеристики

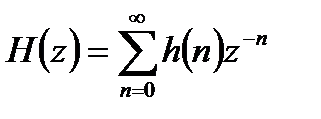(5.11)

представляет собой передаточную функцию ЛДС.

При известной передаточной функции 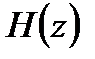импульсная характеристика находится с помощью обратного z – преобразования:

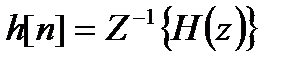. (5.12)

Связь передаточной функции с разностным уравнением

Применим z – преобразование к разностному уравнению

.

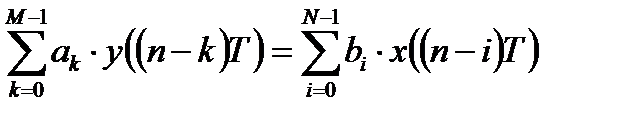Учитывая свойство z – преобразования по запаздыванию, можно получить передаточную функцию ЛДС общего вида:

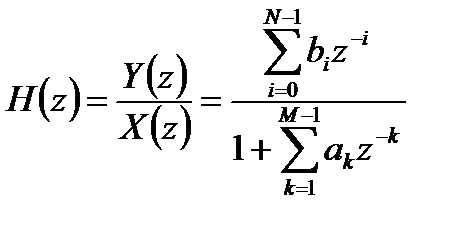. (5.13)

Таким образом, передаточная функция ЛДС представляет собой дробно-рациональную функцию, числитель и знаменатель которой описываются многочленами аргумента 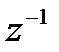с вещественными коэффициентами.

Как любая дробно-рациональная функция, передаточная функция ЛДС характеризуется полюсами и нулями.

Нулями называют значения 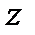, при которых передаточная функция равна нулю.

Полюсами называют значения 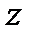, при которых знаменатель передаточной функции равен нулю.

Разновидности передаточных функций

Одна из эквивалентных форм записи передаточной функции выглядит следующим образом

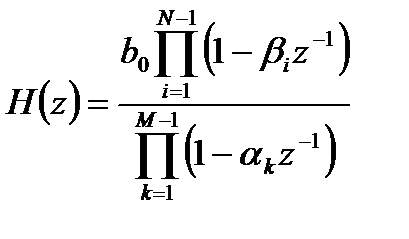, (5.14)

где 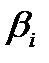- нули, 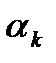- полюса.

Нули и полюса передаточной функции могут быть либо вещественными, либо составлять комплексно-сопряженные пары. Коэффициент усиления 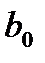всегда вещественный.

Третий вариант представления передаточной функции в виде суммы простых дробей ( :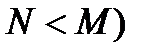

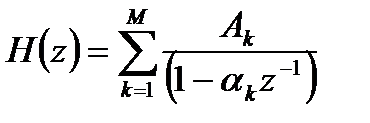, (5.15)

где 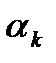- полюс;

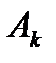- коэффициент разложения при k-м полюсе.

Оценка устойчивости ЛДС по ее передаточной функции

Обратное z – преобразование передаточной функции в виде суммы простых дробей позволяет в общем случае найти импульсную характеристику, так как каждому слагаемому выражения (5.15) соответствует по таблице соответсвий обратное преобразование вида :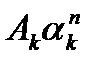

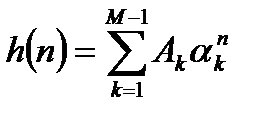. (5.16)

Ряд (5.16) будет сходиться и ЛДС будет устойчива, если выполняется условие:

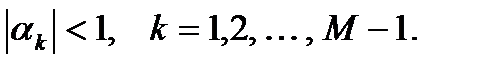(5.17)

Следовательно, чтобы ЛДС была устойчива, необходимо и достаточно, чтобы все полюса ее передаточной функции распределялись внутри единичного круга комплексной z-плоскости.