Лінійні коливальні системи без тертя

Вільні коливання систем з одним ступенем свободи

Якщо положення системи в будь-який момент часу може бути списано єдиним параметром, то система має один ступінь свободи. Прикладами таких систем є: маятник, що коливається в заданій площині (рис.1.1), маса, пов'язана з пружиною (рис. 1.2),

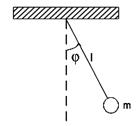
Рисунок 1.1 – Математичний маятник

Рисунок 1.2 – Пружинний маятник

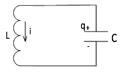
Рисунок 1.3 – Коливальний контур

або електричний контур (рис.1.3), де єдиний параметр (узагальнена координата 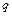) : 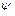– кут відхилення, 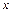- зміщення вантажу, заряд 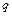на пластинках конденсатора (або 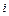- струм в котушці) відповідно.

Для визначеності розглянемо рух маятника. Рівняння руху його запишеться у вигляді

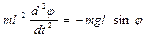(1.1)

і являє собою нелінійне диференціальне рівняння.

Зазвичай нелінійні диференціальні рівняння в аналітичній формі вирішуються важко. Більше того, вони не мають властивості суперпозиції.

Лінійні коливальні системи без тертя

Скористаємося в рівнянні (1.1) розкладанням в ряд Тейлора

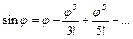(1.2)

Для достатньо малих 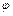можемо знехтувати в (1.2) усіма членами, за винятком 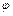. Після спрощення рівняння отримаємо основне диференціальне рівняння задачі про вільні коливання:

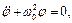(1.3)

де

Загальне рішення цього рівняння має вигляд

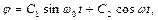
який і висловлює принцип суперпозиції коливань в лінійних системах.

Можна користуватися і іншою формою запису рішення:

(1.4)

яке представляє собою незгасаючі гармонійні коливання. Тут 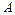– амплітуда коливань, 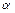– початкова фаза, які знаходяться за початковими умовами. Кругова частота 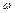пов'язана з фізичними параметрами системи і не залежить від початкових умов. З цієї причини її називають власноючастотою системи.