ПРОСТРАНСТВЕННЫЙ ДЕКРЕМЕНТ ПОЛЯ НЕЙТРОНОВ В СИСТЕМЕ СКВАЖИНА—ПЛАСТ

Как показывают результаты многочисленных эксперимен­тальных исследований и численных расчетов, наиболее устой­чивым для системы скважина — пласт является характер за­висимости показаний детектора от размера зонда Z. Незави­симо от вида генерируемого и регистрируемого излучения (нейтроны, гамма-кванты), конструкции прибора и скважины, типа ее заполнения и положения прибора в ней, минерального состава скелета породы, ее пористости и типа флюида, заполняющего емкостное пространство, показания детектора всегда убывают с увеличением размера зонда Z:

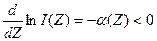. (9.193)

Это — устойчивая закономерность, общая для всех актив­ных (использующих внешние, не присущие самой горной по­роде, источники излучения) ядерно-физических методов иссле­дования горных пород. Функция a(Z) сравнительно слабо из­меняется с изменением Z и стремится к константе (зависящей от свойств пласта) с увеличением размера зонда, j Величина a(Z) — это физический параметр системы скважина — пласт — декремент пространственного (по оси Z) из­менения в скважине поля излучения, сформированного пластом с фиксированными физическими свойствами. Для двухзондовых (и многозондовых) приборов эта величина может быть непосредственно измерена и становится интерпретационным пара­метром, позволяющим количественно охарактеризовать петрофизические свойства пласта.

Уравнение (109) можно рассматривать как алгоритм определения декремента затухания стационарного поля излучения в скважине:

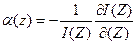. (9.193’)

Закон изменения показаний детектора в зависимости от размера зонда Z в общем случае имеет вид

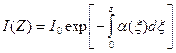. (9.194)

Предэкспоненциальный множитель I₀ представляет собой показания прибора на нулевом зонде (Z=0). Эта величина пропорциональна мощности источника Q и эффективности де­тектора и зависит от свойств пласта, скважинных условий из­мерений и конструкции прибора.

Введем в системе скважина — пласт цилиндрические коор­динаты (r, ξ, φ), совместив полярную ось с осью цилиндриче­ских зон (для простоты все зоны считаем коаксиальными), и функцию Ф(r, ξ, φ | Z) — такую, что произведение dФ(r, ξ, φ | Z)dV определяет вклад излучения выделенного объема dV= 2πrdrdφdξ радиуса r толщиной dr высотою dξ и центральным углом при вершине φ , около точки (r, ξ, φ) в показания детектора на зон­де Z. Величина dФ соответствует абсолютному вкладу в пока­зания детектор излучения, прошедшего из источника в элемент объема dV, аиз него — на детектор через соответствующие промежуточные среды (зоны) и не испытавшего взаимодействия более удаленных (чем dV) объемах среды.

Тогда показание прибора записывается виде

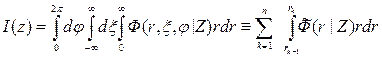, (9.195)

где для краткости обозначено

,

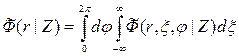и суммирование распространено на все цилиндрические зоны, характеризующиеся радиальной однородностью физических свойств. Предполагается что свойства всех зон, включая зону проникновения и неизменную часть пласта, не изменяются вдоль оси ξ.

Каждое слагаемое в (111) соответствует абсолютному вкладу в показание детектора излучения, приходящего из цилиндри­ческого слоя радиально-однородной среды, заключенной между цилиндрическими поверхностями радиусов r_k-1 и r_h.

Введем функцию

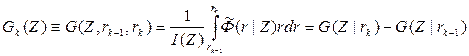, (9.196)

R — радиусы образующих цилиндрического слоя к-той зоны. Она имеет смысл интегрального радиального геометрического фактора к- той цилиндрической зоны. Величина G_h(Z) представляет собой относительный интегральный вклад излучения, приходящего из радиально-однородного цилиндрического слоя толщиной (r_k-r_k-1) в детектор, т.е. определяет влияние k-го слоя (зоны) по его вкладу в результирующее показание детектора.

Величина

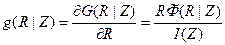(9.196’)

определяет относительный дифференциальный вклад в показания детектора от элементарного цилиндрического слоя единич­ной толщины на расстоянии R от оси прибора. Она имеет смысл дифференциального геометрического фактора элементарного цилиндрического слоя единичной толщины.

Из равенства (9.195) и определения (9.196) следует соотно­шение

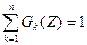. (9.197)

Применим теперь к выражению (111) общий алгоритм (109') определения декремента затухания α(Z) стационарного поля. Выполнив в (111) дифференцирование по параметру Z под знаком интеграла, найдем.

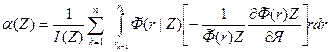(9.198)

Очевидно, что величина Ф(r|Z)(r_k-1≤r≤r_k) зависит не только от физических свойств пласта, но также от геометриче­ских и физических характеристик остальных зон, формирующих поле излучения в рассматриваемой системе. Можно предположить¹, однако, что в пределах каждой зоны соответствующий:

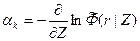, r_k-1 ≤ r ≤ r_k (9.199)

определяется только ее физическими свойствами и в силу радиально-осевой однородности зоны не зависит от переменных (r, Z). Это значит, что функция Ф приближенно представи­ма в виде

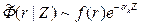, r_k-1 ≤ r ≤ r_k

где

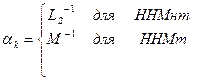(9.200)

(L_s, M,- длины замедления и миграции надтепловых и тепловых нейтронов).

На основании (9.198), (9.199) и (9.196) получим

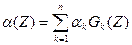(9.201)

Таким образом, результирующий декремент затухания α(Z) аддитивен относительно декрементов затухания в каждой из выделенных зон, взвешенных с соответствующими функциями влияния G_k. Ниже рассмотрим свойства этих функций, которые имеют смысл относительных вкладов излучений зон в результирующие показания.