Создание объектов. Конструктор

Объект— это переменная типа класс. Класс — это абстрактное понятие, шаблон, заготовка для создания объекта. Оперативная память для класса, как и для другого типа, не отводится. Объект существует реально, физически после его создания, то есть он занимает определённую оперативную память.

Объявляется объект одним из следующим способов:

· имя_класса имя_объекта (параметры), если конструктор имеет параметры;

· имя_класса имя_объекта, если конструктор не имеет параметров или все параметры имеют значения по умолчанию или конструктора нет.

В любом случае, во-первых, создаётся объект и, во-вторых, вызывается конструктор, если он есть. В первом варианте конструктору передаются параметры.

Конструктор — это специальная функция, которая служит для инициализации, т. е. задания начальных значений всех (прим. 1) или некоторых (прим. 2) полей класса. В прим. 2 с помощью конструктора задали только размерность массива, а массив определили с помощью функции класса. Теоретически в этой функции разрешается выполнять любые действия, но это делать не рекомендуется. Конструктор обладает следующими особенностями:

· он не имеет никакого типа возвращаемого значения, в том числе void;

· имя конструктора совпадает с именем класса;

· вызывается конструктор автоматически при объявлении объекта. Благодаря последним двум особенностям конструктор обязательно будет выполнен, так как мы не можем забыть объявить объект, а значит вызвать конструктор. В противном случае компилятор напомнит нам об этом.

Конструктор может быть с параметрами или без них. В первом случае число 10 (см. прим. 1) через параметр x передаётся в качестве значения поля a по следующей “цепочке”: 10 –> x –> a. Аналогично число 2 инициализирует поле b: 2 –> y –> b. То есть числа 10 и 2 играют роль фактических параметром при вызове специальной функции, которой является конструктор. При вызове методов повторно передавать эти же значения, как это имело место в случае самостоятельных функций, не членов класса, не надо.

Если конструктор не имеет параметров, то поля класса можно определить с помощью констант. Например, в прим. 1 конструктор может быть таким:

FirstCl { a=2; b=5;}

Тогда вызывается он так: FirstCl obj; т. е. поля из головной функции не передаются, так как они определены с помощью констант в тексте конструктора.

Параметры конструктора, как и любой другой функции (см. §6 гл. 2), могут иметь значения по умолчанию. Например, в первом примере заголовок конструктора может быть таким: FirstCl ( int x=2, int y=5). Его текст при этом не меняется. Тогда объявить объект и вызвать конструктор можно одним из следующих способов:

a) FirstCl obj1; поля получат значения a=2, b=5;

b) FirstCl obj2 (30); значения полей будут такими: a=30, b=5;

c) FirstCl obj3 (30, 40); поля получат значения a=30, b=40;

Конструктор, как и любая другая функция (см. §6 гл. 2), может быть перегружен, то есть можно записать несколько конструкторов, которые отличаются параметрами. Например, в одном и том же классе можно записать два следующих конструктора с одинаковыми, конечно, именами, совпадающими с именем класса:

FirstCl { a=2; b=5;} и FirstCl (int x, int y) { a=x; b=y; };

Тогда объявить объект можно одним из следующих способов:

a) FirstCl obj; при этом поля получат значения 2 и 5;

b) int X, Y ; cin>>X>>Y ; FirstCl obj (X, Y); при этом поля будут проинициализированы введёнными значениями.

Но вместо такой перегрузки конструктора лучше использовать параметры по умолчанию.

Задачи и упражнения.

1. Составить класс для работы с двумя целыми числами. Предусмотреть конструктор, методы для вывода двух чисел, вычисления их суммы, вычисления произведения этих же чисел. В головной функции ввести два числа, создать объект, вычислить и вывести их сумму и произведение. Все методы оформить как внешние.

class firstB

{ int a, b; // поля класса с атрибутом доступа private (частный)

public: // атрибут доступаpublic для методов

firstB(int, int ); // заголовок конструктора с двумя параметрами

void show(); // заголовки остальных функций

long sum();

long mult();

};

firstB:: firstB(int u, int v)

{ a=u; b=v; // текст конструктора

};

// тексты остальных функций, оформленных как внешние

void firstB:: show()

{ cout<<"\nThe first number= "; cout<<a;

cout<<", the second number= "; cout<<b; cout<<endl;

};

long firstB:: sum()

{return a+b;

} ;

long firstB:: mult()

{ return a*b;

};

int main()

{ int A, B; cout<<"A= "; cin>>A; cout<<"B="; cin>>B;

firstB ob (A, B); // создание объекта и передача ему введенных A и B,

// или можно в объект передать константы: firstB ob(5,4);

ob.show(); // вызов метода show

/* Вариант 1: полученные с помощью методов результаты (сумму и произведение), как и для обычных функций, сохраняем в переменных, а затем используем, т. е. выводим.*/

long S, M; S=ob.sum(); M=ob.mult();

cout<<" \nВариант 1: сумма= "<<S<< " произведение= "<<M<<endl;

/* Вариант 2: результаты методов сразу выводим, не сохраняя их в переменных */

cout<<"\nВариант2 :сумма= "<<ob.sum()<<

" произведение= "<<ob.mult();

getch(); return 0;

};

2. Составить класс для работы с двумя целыми числами, предусмотрев вычисление и вывод их суммы и произведения со следующими отличиями, по сравнению с предыдущей программой:

· один и тот же метод и вычисляет, и выводит сумму двух чисел с определенной, указанной в методе, позиции окна. Поэтому этот метод не имеет параметров;

· метод вычисляет и выводит произведение, но позиция вывода передается как параметр метода при ее вызове;

· вывод осуществляется разными цветами, которые, как и исходные числа, являются полями класса. Числа и цвета передаются с помощью конструктора, который поэтому имеет четыре поля;

· все методы встроенные.

class first

{ int a, b, c1, c2;

public:

first(int x, int y, int s1, int s2)

{ a=x; b=y;

c1=s1; c2=s2;

};

void sum()

{textcolor(c1); gotoxy(5,2);

printf("x=%d y=%d sum=%d\n", a, b, a+b);

} ;

void mult(int x, int y)

{ textcolor(c2); gotoxy(x,y);

cprintf("x=%d y=%d mult=%d\n", a, b, a*b);

};

};

int main()

{ first ob (4,5,4,2); ob.sum();

ob.mult(10,6); getch(); return 0;

};

3. Составить класс для работы с одномерным массивом максимальной размерности 10, предусмотрев следующие методы:

· конструктор для проверки и задания размерности массива. Если размерность массива неположительная или больше 10, то работаем с массивом размерности 10;

· ввод массива;

· поиск первого по порядку положительного числа и его индекса.

const nmax=10;

class clarray1

{ int x[nmax]; int n;

public:

clarray1(int v=7)

{ n=v; if (n<1 || n>nmax) n=nmax; };

void myinput()

{ cout<<"Input the array"<<endl;

for (int i=0; i<n; i++)

cin>>x[i];

};

void myfun (int &first, int &ind)

{ for (int i=0; i<n;i++)

if (x[i]>0) { first=x[i]; ind=i;

return;

}

first=-10; ind=-1;

};

};

int main()

{ clrscr(); clarray1 OBJ;

OBJ.myinput(); int F2,I2; OBJ.myfun( F2,I2);

if (F2!=-10)

cout<<" The first positive number= "<<F2<<

" , his index= "<<I2<<endl;

else cout<<" There is not positive number\n";

getch(); return 0;

}

В методе MyInput массив вводим с экрана. Его можно было бы определить и другим способом, например, с помощью датчика случайных чисел.

Размерность массива в конструкторе является параметром по умолчанию. Это означает следующее. При создании объекта можно не передавать размерность, тогда она останется равной 7, т. е. той, которая указана в заголовке функции. Если в головной функции записать, например, clarray OBJ(5), то в объекте, как и раньше, будем работать с массивом размерности 5, которую передали, т. е. параметр по умолчанию 7 изменится.

4. Рассортировать заданный массив точек по возрастанию расстояния до начала координат. Если расстояния одинаковы, то вначале должны быть точки заданной области, а затем — точки, не принадлежащие области. Область ограничена параболой y = x² и прямой y=2.

Составим следующие методы:

· MyInp для ввода координат точек;

· MyPoint для определения расстояния от точки до начала координат и принадлежности точки указанной области;

· ArrPoint для построения массива расстояний и логического массива, определяющего принадлежность каждой точки области;

· RR для перестановки двух величин. Эта функция дважды перегружена для вещественного и логического типов;

· MySort для сортировки массива с использованием функций RR;

· MyOut для вывода координат точек.

const nmax=10;

class clCoord

{ float x[nmax], y[nmax], d[nmax]; bool b[nmax]; int n;

void MyPoint(float x1, float y1, float &d1, bool &b1)

{ d1=sqrt(x1*x1 + y1*y1); b1= y1>=x1*x1 && y1<2;

};

void RR(float &u, float &v)

{ float t; t=u; u=v; v=t; } ;

void RR(bool &u, bool &v)

{ bool t; t=u; u=v; v=t; };

public:

clCoord (int , float [], float []); void ArrPoint();

void MySORT(); void MyOut();

};

clCoord::clCoord (int m, float u[], float v[])

{ n=m; if (n>nmax || n<1) n=nmax;

for(int i=0; i<n; i++)

{ x[i]=u[i]; y[i]=v[i];

}

} ;

void clCoord::ArrPoint()

{ for(int i=0; i<n; i++)

MyPoint (x[i],y[i],d[i],b[i]);

};

void clCoord::MySORT()

{ int k; bool flag; k=n;

do { k--; flag=false;

for(int i=0; i<k; i++)

if ( d[i]>d[i+1] || d[i]==d[i+1] && b[i]>b[i+1])

{ flag=true; RR(x[i],x[i+1]);

RR(y[i],y[i+1]); RR(d[i],d[i+1]);

RR(b[i],b[i+1]); }

} while (flag);

} ;

void clCoord::MyOut()

{ cout<< " \n";

cout<< " T A B L E \n";

cout<< " x y d b \n";

cout<< " \n";

for ( int i=0; i<n; i++)

printf (" %7.2f %7.2f %8.3f %1d \n",

x[i], y[i], d[i], b[i]);

} ;

int main()

{ const N=8;

float X[N]={ 1.1, -0.6, -3.3, 0.45, -0.45, 0.6, 0.7, -0.8},

Y[N]={-1.0, -0.7, 3.2 , 0.45, -0.45, 0.7 , -0.6, 8.1};

clCoord OBJ (N,X, Y); OBJ.ArrPoint ();

clrscr(); OBJ.MyOut();

OBJ.MySORT(); cout<<"\n Press any key\n";

getch(); OBJ.MyOut();

getch(); return 0;

}

Функции MyPoint и RR имеют атрибут доступа private по умолчанию. Они доступны, как и поля, только в функциях этого класса и недоступны в других функциях. Например, из функции main их вызвать нельзя.

Массивы передаются с помощью конструктора через параметры. Определяются массивы в головной функции во время объявления. Здесь их можно ввести или задать с помощью датчика случайных чисел.

5. В предложенном варианте программы четыре цвета передаются в качестве параметров функций outи show. Можнопредложить второй вариант: включаем цвета в класс в качестве двух дополнительных полей наряду с массивом и его размерностью. Тогда функции outи showбудут без параметров, а конкретные цвета передаются c помощью конструктора, как это сделано для размерности массива. Изменить программу 4.

6. Составить класс для работы с одним целым числом. Кроме конструктора предусмотреть следующие методы:

1) вывод числа в разреженном виде, т. е. между каждой десятичной цифрой должен быть один пробел;

2) вывод числа в двоичной системе счисления;

3) вывод числа в шестнадцатеричной системе счисления.

В функции main проверить эти методы.

7. Составить класс для работы с рациональными дробями. Класс содержит в качестве полей два целых числа: числитель и знаменатель. В конструкторе с двумя параметрами предусмотреть проверку знаменателя на нуль. Разработать следующие методы: вывод дроби в виде 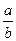; сокращение дроби, например, 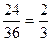; сложение двух дробей; деление двух дробей. В последних двух методах один операнд берется из класса, а второй передается как два параметра метода.

8. Составить класс для работы с моментами времени внутри одних суток. Класс содержит в качестве полей три целых числа: час, минута и секунда. В конструкторе с тремя параметрами выполнить проверку корректности момента времени. Предусмотреть некоторые из следующих методов:

1) вывод момента времени, который будет через S секунд, если S передается как параметр метода. Величина S меньше количества оставшихся до конца суток секунд;

2) определение количества секунд, прошедших с начала суток:

3) вывод момента времени, который был на S секунд раньше, если S передается как параметр метода. Величина S меньше количества прошедших после начала суток секунд;

4) определение количества секунд между двумя моментами времени. Один из них берется из класса, а второй передается как три параметра метода.

9. Составить класс для работы с датами внутри одного года. Класс содержит в качестве полей два целых числа: число и номер месяца. В конструкторе с двумя параметрами выполнить проверку корректности даты. Предусмотреть некоторые из следующих методов:

1) вывод даты следующего дня;

2) получение номера дня недели для заданной даты и вывод его названия (понедельник, вторник …). Считать, что задано, в какой день недели было первое число указанного месяца;

3) вывод даты предыдущего дня;

4) определение количества дней, прошедших с начала года;

5) определение даты, которая будет через D дней, если D передается как параметр метода. Величина D меньше количества оставшихся до конца года дней;

6) определение количества дней между двумя датами. Одна из них берется из класса, а вторая дата передается как два параметра метода.

10. Решить задачу 9, учитывая и год, т. е. класс должен содержать три целых числа: число, номер месяца и год.

11. Составить класс для работы с большими целыми числами, для которых вещественный тип неприемлем, а типа long
недостаточно. Для хранения такого числа предлагается использовать одномерный массив, каждый элемент которого представляет собой одну десятичную цифру числа. Поэтому класс содержит массив и его размерность, т. е. количество цифр числа. Во всех вариантах предусмотреть конструктор, ввод и вывод массива цифр и следующие методы в зависимости от вариантов:

1) увеличение числа на единицу; вычитание двух больших чисел, т. е. вычитание двух массивов по правилу вычитания “в столбик”;

2) уменьшение числа на единицу; сложение двух больших чисел, т. е. сложение двух массивов по правилу сложения “в столбик”;

3) умножение двух больших чисел по правилу умножения “в столбик”;

4) сравнение двух больших чисел;

Замечание. В методах для реализации операций вычитания, сложения, умножения и сравнения двух больших чисел один массив (число) берется из класса, а другой массив (число) передается через параметр метода.

5), 6), 7) сложение (вычитание, умножение) большого числа (массива) с обычным целым числом. Большое число (массив) берем из класса, а обычное, представленное как число типа long, передается как параметр метода. В алгоритме реализации таких методов необходимо предусмотреть выделение из обычного числа типа long цифр и их использование.

12. Решить задачи из гл. 2, составив и используя соответствующие классы.

Глава 4
ПРОСТЫЕ ТИПЫ ДАННЫХ

Целый тип

Битовые операции

В языке С++ есть следующие битовые операции:

& — битовое и;

| — битовое или;

^ — исключающее или;

~ — дополнение;

>> сдвиг вправо на указанное количество разрядов (бит);

<< сдвиг влево на указанное количество разрядов (бит).

Первые три операции являются бинарными. Они работают с двоичным представлением двух операндов (констант, переменных или выражений). Они выполняются над каждой парой битов по следующим правилам:

& | ^

1 1 1 1 0

1 0 0 1 1

0 1 0 1 1

0 0 0 0 0

Упражнение 1. Определить результат:

short int k1=30,k2=-1707,r; r=k1 & k2;

cout<<endl<< k1<< “&”<<k2<<”=”<<r;

1) Представляем положительное число 30 в оперативной памяти. Для этого переводим его в двоичную систему счисления делением на 2 следующим образом: 30/2=15 (0 в остатке), 15/2=7
(1 в остатке), 7/2=3 (1), 3/2=1(1), 1/2=0(1). Записывая все остатки в обратном порядке, получим 30₁₀ =11110₂. Представляем это число в двух байтах, так как оно объявлено как short int. Для этого дописываем слева необходимое количество нулей и получаем 0000000000011110.

2) Представляем отрицательное число –1707 в оперативной памяти в дополнительном коде. Для этого выполняем следующее:

а) так как делением на 2 перевод в двоичную систему счисления выполняется долго, сначала переведём число 1707 во вспомогательную шестнадцатеричную систему счисления делением на 16. 1707/16=106 (11 в остатке), 106/16=6 (10), 6/16=0(6). Записывая все остатки в шестнадцатеричной системе счисления в обратном порядке, получим 1707₁₀ =6AB₁₆, так как 10₁₀=A₁₆, 11₁₀=B₁₆;

б) каждую шестнадцатеричную цифру полученного результата записываем в виде четырёх двоичных цифр (двоичной тетрады): 011010101011;

в) представляем это число в двух байтах, так как оно объявлено как short int. Для этого дописываем слева необходимое количество нулей: 0000011010101011. Получили представление положительного числа в памяти компьютера;

г) для получения дополнительного кода выполняем инверсию положительного представления с учётом “левых” нулей, т. е. нуль меняем на единицу, а единицу на нуль. К результату инверсии прибавляем единицу. Получим 1111100101010101.

3) К полученным таким образом двоичным кодам двух чисел применяем битовую операцию и (&). При этом единицы получаем только там, где были обе единицы, во всех остальных разрядах получатся нули: 00000000000010100.

4) Что это за число в десятичной системе счисления? Для ответа на вопрос разбиваем его на тетрады и получаем число в шестнадцатеричной системе счисления: 14₁₆. Для перевода в десятичную систему счисления записываем его как сумму степеней числа 16, умноженную на соответствующую шестнадцатеричную цифру: 14₁₆=1*16+4=20₁₀. При этом действия выполняются в десятичной системе счисления.

Упражнение 2. Найти r2=30 | -1707, если, a) short r2, b) unsigned short r2.

По умолчанию подразумевается тип int. К полученным в предыдущем упражнении двоичным кодам применяем битовую операцию или ( | ). При этом нули получаются только там, где были оба нуля, во всех остальных разрядах получатся единицы: 1111100101011111.

a) Так как результат объявлен как знаковое число (по умолчанию signed) и в самом левом бите получилась единица, то это дополнительный код отрицательного числа. Для его получения выполняем в обратном порядке то, что делали в пункте 2) предыдущего упражнения: вычитаем единицу и выполняем инверсию. Получим 0000011010100001. Разбив на тетрады, получаем 6A1₁₆=6*16²+10*16+1=1697. Ответ: –1697.

б) Так как при таком объявлении (unsigned) отрицательного числа быть не может, то мы имеем положительное число, несмотря на единицу в самом левом бите. Разбиваем двоичное число на тетрады и переводим его из шестнадцатеричной системы счисления в десятичную: F95F₁₆=15*16³+9*16²+5*16+15=63839.

Упражнение 3.Найти r3=30 ^ –1707, если: a) short r3, b) unsigned short r3.

Упражнение 4.Пусть short r3. Определить результат: r3=~30.

Операция дополнение (~) меняет единицу на нуль, а нуль на единицу. Поэтому к полученному в упр. 1 двоичному коду числа 30 0000000000011110 применяем инверсию: 1111111111100001. Так как по умолчанию переменная имеет модификатор signed и в самом левом бите получена единица, то это отрицательное число. Для его восстановления вычитаем единицу и выполняем инверсию: 0000000000011111=1F₁₆=1*16+15=31. Ответ: –31.

Операция << (сдвиг влево) имеет общий вид a<<m, где a — число, участвующее в сдвиге, а m показывает, на какое количество разрядов сдвигаем число. При этом как для положительных, так и для отрицательных чисел “вращение”, или циклический сдвиг, не выполняется. Значения левых сдвинутых бит теряются, а справа появляются нули.

Например, в результате выполнения следующего фрагмента программы

char k= –5;

for(int I=1; I<=4; I++)

{ k<<=1; // или k=k<<1;

printf("%5d",k);

}

получим –10, –20, –40, –80. Почему? Число –5 имеет следующее представление в одном байте (тип char): 11111011. После сдвига на один разряд имеем 11110110. При этом левая крайняя единица потерялась, и справа появилось число 0, а не 1. Так как это отрицательное число, то после вычитания единицы и инверсии получаем 00001010, т. е. число 10. Поэтому первым будет выведено число
–10. Аналогично получаем остальные числа.

Сдвиг влево на один разряд означает увеличение целого числа в два раза, сдвиг влево на два разряда увеличивает число в четыре раза и так далее, сдвиг влево на m разрядов равносилен увеличению числа в 2^m раза. Это не зависит от того, какое число, положительное или отрицательное, участвовало в сдвиге.

Сдвиг вправо (a >> m) выполняется аналогично, без циклического сдвига. При сдвиге положительных чисел слева появляется m нулей, а при сдвиге отрицательных чисел слева добавляется m единиц.

Сдвиг вправо на один разряд означает целочисленное деление на 2, сдвиг вправо на два разряда означает целочисленное деление на 4 и так далее, сдвиг вправо на m разрядов равносилен целочисленному делению числа на 2^m .

Например, 42>>2 даёт 10₁₀. Действительно, 42=00101010₂, а в результате сдвига получаем 00001010₂=10₁₀. В результате операции –42>>2 получим –11. Почему? –42=11010110₂, а после сдвига получим 11110101₂, то есть отрицательное число –11.

В качестве упражнениявыполните следующий фрагмент программы и объясните результат:

char k= –30; cout<<endl;

for(int I=1; I<=4; I++)

{ k>>=1; // или k=k>>1;

printf ( "%5d" , k);

}