Проблема синтеза надёжных схем из ненадёжных элементов
Рассмотренные ранее методы синтеза схем ЦА исходят из задачи наиболее экономного расходования элементов, как ЗЭ так и ЛЭ. По самому определению наиболее экономной схемы она должна обладать тем свойством, что выход из строя любого её элемента вызывает выход из строя всей схемы в целом, потому что, если в схеме есть элементы, которые могут исключить, не нарушая работы схемы, то такая схема не будет минимальной по числу элементов, использованных при её построении.
Различают 2 вида неисправностей ЦА. Неисправность первого вида – отказ, состоит в том, что начиная с некоторого момента времени и во все последующие моменты времени элемент перестаёт функционировать или функционирует неверно. Второй вид неисправности – это мгновенная самоустраняющаяся неисправность, называемая сбоем. наступление сбоя означает, что элемент не сработал или неправильно сработал в течение одного такта работы автомата, но возникшая таким образом неисправность вовсе не должна сохраняться на протяжении последующих тактов.
Современные сложные электронные ЦА состоят из многих тысяч ЛЭ и ЗЭ, требования к надёжности их работы очень высоки (вероятность сбоя ЦА должно быть 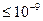 ), вероятность сбоя отдельных элементов
), вероятность сбоя отдельных элементов 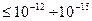 . В ряде случаев требования к надежности элементов оказываются практически невыполнимыми, и тогда возникает проблема построения высоконадёжных схем из относительно ненадёжных элементов.
. В ряде случаев требования к надежности элементов оказываются практически невыполнимыми, и тогда возникает проблема построения высоконадёжных схем из относительно ненадёжных элементов.
Методы на которых основано решение этой проблемы, сводятся к дублированию одних элементов другими, к многократному повторению, к автоматическому контролю и к исправлению работы отдельных участков схемы или всей схемы в целом.
Наиболее распространёнными является дублирование. Способ дублирования ЦА сводится к замене одного автомата двумя одинаковыми автоматами, выходы которых в процессе функционирования дублируемых автоматов постоянно сравниваются с помощью специальной схемы сравнения. Дублирование не учитывает внутреннюю структуру ЦА; с его помощью обнаруживаются ошибки любой кратности, возникающие на выходах одного из дублируемых устройств, а также ошибок, возникающие на выходах двух устройств одновременно, приводящие к появлению неодинаковых векторов выходов дублируемых устройств.
Недостатки дублирования:
- большая структурная избыточность требующая усвоения оборудования.
Пример: Продублировать ЦА А, имеющий три выходных канала 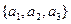 .
.
 Состояние выходов продублированного устройства можно представить в виде матрицы G при контроле:
Состояние выходов продублированного устройства можно представить в виде матрицы G при контроле:
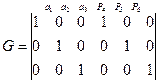 ,линейный групповой код
,линейный групповой код
а так называемая функция декодирования 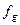 имеет вид:
имеет вид:
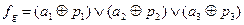
Дублирование можно осуществить не пространственным, а временным путём, то есть производить многократную прогонку входного слова через один и тот же ЦА и принимать в качестве верных лишь достаточно часто повторяющиеся результаты.
Другой распространённый метод – мажорирование. Мажорирование позволяет вырабатывать правильный выходной сигнал при наличии неисправностей в ЦА и определять место их появления с точностью до указания номеров неправильно работающих устройств. Мажорирование требует для своей организации использования нечётного числа устройств, работающих параллельно. Выработка правильного выходного сигнала устройства осуществляется мажоритарным ЛЭ. Для определения номеров неправильно работающих устройств необходимо дополнительно иметь специальный элемент анализа (ЭА).
Пример: Выполнить мажорирование для ЦА 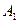 с одним выходом
с одним выходом 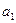 .
.
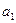
| 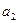
| 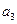
| f | 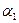
| 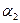
| 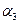
|

f – выход устройства, 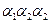 - выходы элемента анализа.
- выходы элемента анализа.
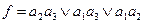
для ЭА: 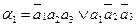
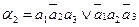
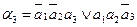
Недостаток метода – большая структурная избыточность.
С целью увеличения надёжности ЦА употребляются также специальные методы кодирования, позволяющие автоматически обнаруживать и даже исправлять ошибки, получающиеся в результате сбоев.
В большинстве современных ЦА информация делится на слова, имеющие определённую длину. Добавляя в коды этих слов новые разряды, и использовать их для хранения информации, позволяющей обнаруживать и исправлять ошибки в коде, возникающие в результате сбоев. Такие удлинённые коды являются избыточными, то есть они содержат большее число разрядов, чем необходимо для представления имеющейся информации.
Различают избыточные коды с обнаружением ошибок и избыточные коды с исправлением ошибок (самокорректирующиеся коды).
Простейший избыточный код – код с проверкой на чётность. Такой код получают путём добавления к слову одного контрольного разряда, в который записывают 0 или 1 с тем, чтобы число 1 в полученной кодовой комбинации было нечётным. Если, например, исходное слово А=10101100, то в коде с проверкой на чётность оно будет представлено как A`=101011001. Если А=10101101, то A`=101011010.
Таким образом любая ошибка нечётной кратности обнаруживается этим кодом.
К кодам с исправлением ошибок относятся коды Хэмминга, предназначенные для исправления одной ошибки или обнаружения двух и исправления одной ошибки. (см. К.Г.Самофалов ЭЦВМ стр.466).
Коды Хэмминга
Коды позволяют исправлять одну ошибку в слове или обнаруживать две и исправлять одну ошибку.
Такие коды имеют несколько контрольных разрядов (КР), каждый из которых контролирует по чётности свою группу разрядов в слове. Эти группы формируются так, чтобы исследовательный опрос КР указал место сбоя. В КР записывается такая цифра, чтобы количество “1” в контролируемых разрядах было нечётным.
Представим кодовую комбинацию с числом разрядов n=15. Тогда схема формирования КР в коде Хэмминга имеет вид:
| Контрольные разряды | Номера разрядов | ||||||||||||||
| A | x | x | x | x | x | x | x | x | |||||||
| B | x | x | x | x | x | x | x | x | |||||||
| C | x | x | x | x | x | x | x | x | |||||||
| D | x | x | x | x | x | x | x | x |
КР А контролирует по чётности все нечётные разряды кода. В КРА записывается такая цифра, чтобы количество “1” в нечётных разрядах было нечётным. Таким образом КРА контролирует по чётности все разряды в номерах которых есть “1” в первом разряде (в двоичном представлении).
КР В контролирует по чётности разряды в номерах которых есть “1” во втором разряде.
КР С контролирует по чётности разряды в номерах которых есть в третьем разряде.
КР Д контролирует по чётности разряды в номерах которых есть в четвёртом разряде.
Контрольные разряды могут быть размещены среди информационных различными способами. Наиболее удобно их размещать на 1,2,4,… 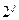 позициях, так как в этом случае каждый КР принадлежит только одной, соответствующей ему группе разрядов.
позициях, так как в этом случае каждый КР принадлежит только одной, соответствующей ему группе разрядов.
Если число КР=К, то длина кодовой комбинации n определяется таким образом:
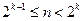 ,
,
при k=4 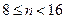 . Отсюда можно найти k
. Отсюда можно найти k 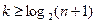 , так как при работе кода возможны n+1 результатов: ошибки нет, ошибка в 1-м разряде, во 2-м разряде и так долее.
, так как при работе кода возможны n+1 результатов: ошибки нет, ошибка в 1-м разряде, во 2-м разряде и так долее.
Пример 1. сформируем КР для слова х=01110100101. Длина слова m=11, k=4, n=15. следовательно код Хэмминга должен иметь вид:
АВ0С111D0100101
Для определения значений А, В, С, D решим уравнения:
А+0+1+1+0+0+1+1=1 (mod 2)=1 А=1
В+0+1+1+1+0+0+1=1 (mod 2)=1 В=1
С+1+1+1+0+1+0+1=1 (mod 2)=1 С=0
D+0+1+0+0+1+0+1=1 (mod 2)=1 D=0
Таким образом, слово х в коде Хэмминга примет вид: 110011100100101.
Пример 2. найти ошибку в слове х=110011100101101. для этого сформируем суммы по mod 2 разрядов, контролируемых разрядами А, В, С,D.
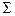 A=1+0+1+1+0+0+1+1 (mod 2)=1
A=1+0+1+1+0+0+1+1 (mod 2)=1 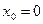
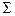 B=1+0+1+1+1+0+0+1 (mod 2)=1
B=1+0+1+1+1+0+0+1 (mod 2)=1 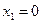
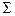 C=0+1+1+1+1+1+0+1 (mod 2)=0
C=0+1+1+1+1+1+0+1 (mod 2)=0 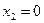
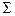 D=0+0+1+0+1+1+0+1 (mod 2)=0
D=0+0+1+0+1+1+0+1 (mod 2)=0 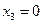
Следовательно, ошибка в разряде с номером 1100. Если ошибки нет, то проверка по всем КР даёт номер разряда 0000, которой нет.
Пример 3. Сформируем 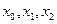 при наличии ошибок во 2-м и 5-м разрядах слова х=1110001, то есть принято слово x`=1010101.
при наличии ошибок во 2-м и 5-м разрядах слова х=1110001, то есть принято слово x`=1010101.
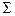 A=1+1+1+1 (mod 2)=0
A=1+1+1+1 (mod 2)=0 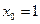
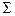 B=0+1+0+1 (mod 2)=0
B=0+1+0+1 (mod 2)=0 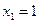
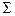 C=0+1+0+1 (mod 2)=0
C=0+1+0+1 (mod 2)=0 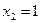
Таким образом, при двукратной ошибке декодирование даёт номер разряда 111, что неверно.
Незначительное увеличение избыточности кода путём введения дополнительного КР1, осуществляющего проверку на чётность всего кода, позволяет обнаружить все двукратные ошибки. Располагает КР1 на месте “0”–го разряда кода. Признаком наличия двукратной ошибки является равенство нулю функции x` при проверке всех разрядов кода на нечётность и равенство “1” хотя бы одной функции 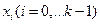 .
.
Пример 4. Найдём КР1 для слова х=1110001.
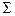 A=1+1+0+1=1
A=1+1+0+1=1 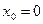
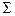 B=1+1+0+1=1
B=1+1+0+1=1 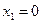
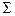 C=0+0+0+1=1
C=0+0+0+1=1 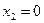
I+1+0+0+1 (mod 2)=1 I=1
Таким образом, слово примет вид 11110001.
Пусть принято слово x`=11010101 ошибки во 2-м и 5-м разрядам. Сформируем функции 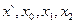 .
.
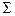 A=1+1+1+1 (mod 2)=0
A=1+1+1+1 (mod 2)=0 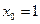
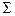 B=0+1+0+1 (mod 2)=0
B=0+1+0+1 (mod 2)=0 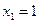
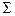 C=0+1+0+1 (mod 2)=0
C=0+1+0+1 (mod 2)=0 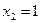
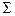 I=1+1+0+1+0+1+0+1=1 x`=0
I=1+1+0+1+0+1+0+1=1 x`=0
Таким образом, в коде присутствуют 2 ошибки.
Общий недостаток избыточных кодов – они не приспособлены для выполнения арифметической операции.
Глава 14
Дата добавления: 2016-07-18; просмотров: 1452;











