Проектирование КС на ПЛМ
Под ПЛМ понимают конструктивный элемент двухступенчатой структуры, изготавливаемый в виде программируемой БИС. Настройка (программирование) ПЛМ осуществляется пользователем с помощью специального оборудования (программатора) и заключается в устранении некоторых связей посредством фотошаблонов или выжиганием диодных перемычек. Такая ПЛМ называется ( 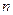 ,
, 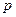 ,
, 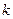 ) - ПЛМ, где n - число входов ПЛМ; p - число выходов ПЛМ, k - число конъюнкций, реализуемых ПЛМ. Входы и выходы ПЛМ называются столбцами, а конъюнкции строками. Рассматриваемая ПЛМ содержит (
) - ПЛМ, где n - число входов ПЛМ; p - число выходов ПЛМ, k - число конъюнкций, реализуемых ПЛМ. Входы и выходы ПЛМ называются столбцами, а конъюнкции строками. Рассматриваемая ПЛМ содержит ( 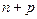 ) столбцов и k строк. Число
) столбцов и k строк. Число 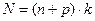 называется площадью ПЛМ.
называется площадью ПЛМ.
 ПЛМ можно представить в виде двух матриц. Матрица М1 (матрица И) реализует k возможных конъюнкций от n - переменных, матрица М2 (матрица ИЛИ) реализует возможных дизъюнкций от k - переменных (не более чем от k).
ПЛМ можно представить в виде двух матриц. Матрица М1 (матрица И) реализует k возможных конъюнкций от n - переменных, матрица М2 (матрица ИЛИ) реализует возможных дизъюнкций от k - переменных (не более чем от k).
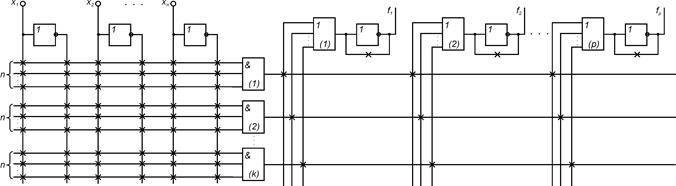
Пусть необходимо реализовать систему функций
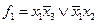 ;
;
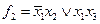 .
.
Электрическая принципиальная схема описывается уравнениями:
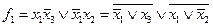 ;
;
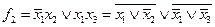 .
.
Функциональная схема реализации системы функций
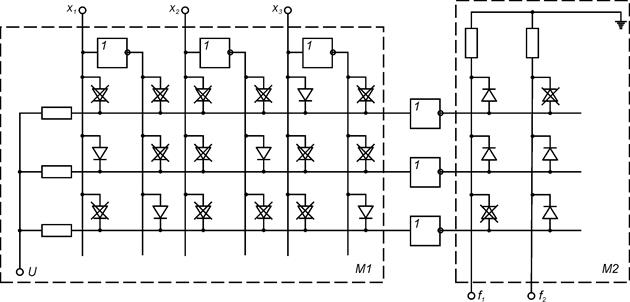
Электрическая схема реализации системы функций
Различают две задачи синтеза КС на ПЛМ:
1) заданна система булевых функций. Надо реализовать её на ПЛМ, минимизируя суммарную площадь ПЛМ. Задача решается на БИС, структуру которых определяет заказчик;
2) реализация КС, соответствующей системе булевых функций на минимальном числе ПЛМ с заданными параметрами ( 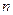 ,
, 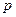 ,
, 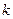 ).
).
Глава 12
Канонический метод структурного синтеза ЦА с памятью
Канонический метод структурного синтеза ЦА с памятью позволяет свести задачу структурного синтеза произвольного ЦА с памятью к задаче синтеза комбинационных схем. Этот метод оперирует с элементарными автоматами двух классов: элементарными автоматами с памятью (элементы памяти) и элементарными комбинационными автоматами (логические элементы).
Результатом работы метода являются уравнения булевых функций автомата в канонической форме представления. Исходными данными для начала работы служит абстрактный автомат ЦА с памятью. Канонический метод можно условно разделить на следующие этапы:
1) кодирование;
2) выбор элементов памяти автомата;
3) выбор структурно-полной системы элементов;
4) построение уравнений булевых функций выходов и возбуждения ЦА;
5) построение функциональной схемы ЦА.
Кодирование
Абстрактный ЦА может быть описан в виде 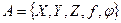 .
.
При переходе на структурный уровень представления каждая буква 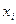 входного алфавита
входного алфавита 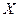 автомата, представляется как двоичный набор (вектор), число компонентов которого равно числу физически реализованных элементарных входных каналов структурного автомата, т.е. каждая буква
автомата, представляется как двоичный набор (вектор), число компонентов которого равно числу физически реализованных элементарных входных каналов структурного автомата, т.е. каждая буква 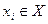 кодируется двоичным вектором. Минимальное число физически реализованных элементарных входных каналов
кодируется двоичным вектором. Минимальное число физически реализованных элементарных входных каналов 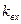 в автомате может быть определено по формуле
в автомате может быть определено по формуле 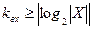 , где
, где 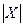 - мощность входного алфавита
- мощность входного алфавита 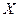 . Если
. Если 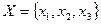 , то
, то 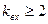 , т.е. каждая буква
, т.е. каждая буква 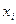 кодируется двоичным вектором, состоящим из двух компонент, например
кодируется двоичным вектором, состоящим из двух компонент, например 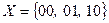 . Минимальное число элементарных выходных каналов
. Минимальное число элементарных выходных каналов 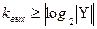 . Для множества состояний
. Для множества состояний 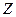
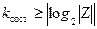 .
.
Процесс замены букв алфавита 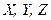 абстрактного автомата двоичными векторами называется кодированием и может быть описан таблицами кодирования.
абстрактного автомата двоичными векторами называется кодированием и может быть описан таблицами кодирования.
Пример: Абстрактный автомат Мили задан совмещенной таблицей переходов-выходов 1. Кодирование букв алфавита 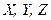 , представлено таблицами 2, 3, 4. При этом
, представлено таблицами 2, 3, 4. При этом 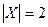 ,
, 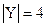 ,
, 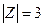 ,
, 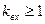 ,
, 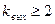 ,
, 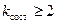 .
.
Таблица 1
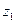 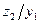 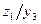
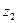 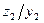 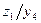
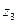 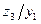 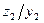
| Таблица 2
вх. сигн. код
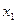 
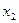 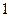
| Таблица 3
вых. сигн. код
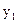 
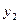 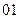
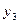 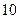
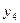 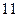
| Таблица 4
состояния код
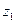 
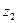 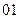
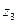 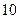
|
Таблица 5
| входные сигналы | |||
| 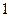
| ||
| состояния | 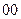
| 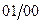
| 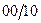
|
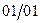
| 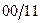
| ||
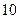
| 10/00 | 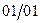
|
Каждой кодируемой букве может быть приписан произвольный двоичный вектор, но обязательно две различные буквы (одного алфавита) должны кодироваться различными двоичными векторами. Получением структурной таблицы переходов-выходов автомата (табл. 5) заканчивается это кодирование.
12.2 Выбор элементов памяти автомата
Замена таблиц переходов ЦА на структурную таблицу переходов приводит к тому, что функция переходов 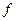 ЦА становится векторной. В соответствии со структурной таблицей переходов ЦА его векторная функция
ЦА становится векторной. В соответствии со структурной таблицей переходов ЦА его векторная функция 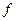 каждой паре двоичных векторов
каждой паре двоичных векторов 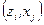 ставит в соответствие определенный двоичный вектор
ставит в соответствие определенный двоичный вектор 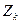 , что определяется соотношением
, что определяется соотношением 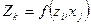 . Из этого следует. Что структурный автомат должен запоминать двоичный вектор каждого очередного состояния ЦА, для чего служат элементы памяти.
. Из этого следует. Что структурный автомат должен запоминать двоичный вектор каждого очередного состояния ЦА, для чего служат элементы памяти.
При каноническом методе структурного синтеза автоматов в качестве элементов памяти используются элементарные автоматы Мура с двумя состояниями, обладающие полной системой переходов и выходов.
Полнота системы переходов-выходов для любой пары состояний ЦА существует входной сигнал, переводящий ЦА из одного состояния в другое.
Полнота системы выходов – различным состояниям автомата соответствуют различные выходные сигналы; обычно нулевому состоянию 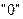 элементарного автомата соответствует нулевой выходной сигнал
элементарного автомата соответствует нулевой выходной сигнал 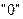 , а единичному состоянию - единичный выходной сигнал
, а единичному состоянию - единичный выходной сигнал 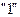 .
.
Число элементов памяти структурного автомата равно числу компонент вектора его состояний.
В качестве элементов памяти структурного автомата обычно используются D -, T -, RS - и JK - триггеры, удовлетворяющие требованиям относительно полноты переходов и выходов. Каждый из приведенных триггеров является автоматом Мура. Входы D, T, RS и JK называются информационными. Таблицы переходов триггеров составляются только для информационных входов. Остальные входы являются вспомогательными (C, R, S). Каждый триггер имеет два выхода 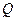 и
и 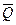 .
.
 |
 
|
Дата добавления: 2016-07-18; просмотров: 2284;












