Построение функциональной схемы автомата

На основании полученных выражений для булевых функций возбуждений элементов памяти автомата и булевых функций выходов автомата строятся КС функций возбуждения и КС формирования выходных сигналов. Элементы памяти подключаются к построенным КС. Функциональная схема автомата Мили при использовании Т-триггера представлена на рис. 1, D-триггера – на рис. 2, RS-триггера – на рис. 3, JK-триггера – на рис.4.

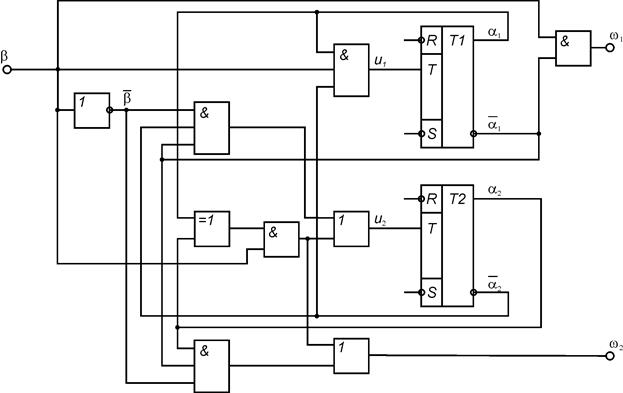
Рис. 12.5.

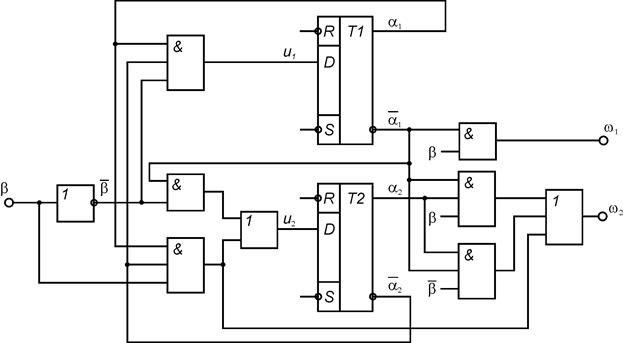
Рис. 12.6.

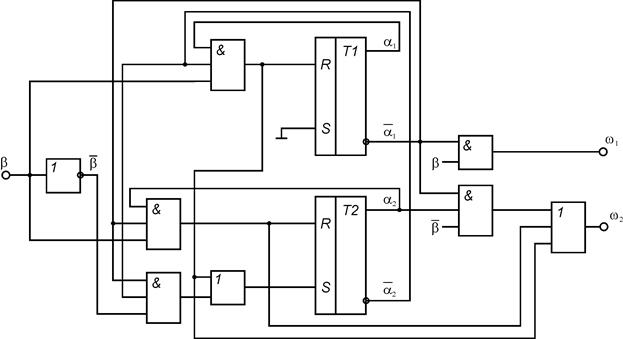
Рис. 12.7.

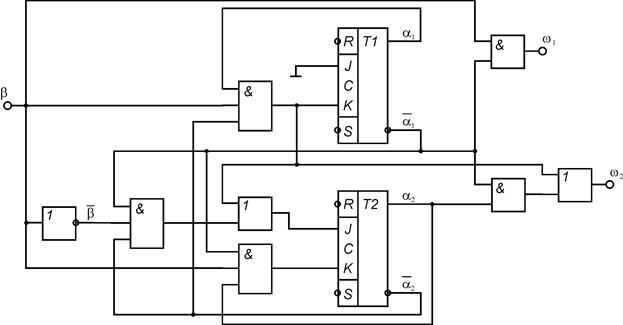
Рис. 12.8.

Глава 13

Обеспечение устойчивости функционирования ЦА

Обеспечение устойчивости функционирования ЦА с памятью – одна из главных задач этапа структурного синтеза. Под устойчивым функционированием ЦА понимают его функционирование в соответствии с таблицей переходов и выходов. Неустойчивая работа ЦА связана с особенностями физической реализации ЛЭ и элементов памяти его схемы, а так же различными величинами задержек распространения сигнала в элементах и КС.

По характеру физических сигналов, которые используются в ЦА может выделить три основных типа схем: потенциальные, импульсные и импульсно-потенциальные.

Потенциальные схемы может быть построены как на принципе естественного тактирование (асинхронные схемы), так и на принципе принудительного тактирование (синхронные схемы). При естественном тактировании выходы ЗЭ (элементов задержки) через схему обратной связи (составленную из ЛЭ) управляют своими собственными входами. Это создаёт возможность появления в схеме “гонок”. Суть гонок состоит в следующем: ЗЭ (элементы задержки) имеют различные, хотя и близкие времена срабатывания. Если по условиям срабатывания (таблице переходов) ЦА в какой-то момент времени должен изменить свое состояние сразу несколько ЗЭ, то между элементами начинаются гонки. Тот элемент, который выиграет эти гонки, то есть изменит свое состояние раньше, чем другие элементы, может через цепь обратной связи изменить сигналы на входах некоторых ЗЭ до того, как другие участвующие в гонке элементы изменят свое состояние. Это может вызвать переход автомата совсем не в то состояние, которое предусмотрено таблицей переходов автомата.

Проблему гонок может решить за счёт исключения необходимости одновремённого изменения состояний сразу у нескольких ЗЭ. С этой целью применяют противогоночное кодирование состояний ЦА, при котором (двоичные) коды любых двух соседних состояний (состояний переходящих одно в другое под воздействием какого-нибудь входного сигнала) отличаются друг от друга не более чем одним разрядом. Но противогоночное кодирование оказывается возможным далеко не во всех случаях.

Необходимость решения проблемы гонок и проблемы согласования переходов ЦА из одного состояния в другое с изменениями входных сигналов отпадает при введении принудительного тактирования автомата, то есть при превращение автомата в синхронный автомат. Для потенциальных схем принудительное тактирование осуществляется за счёт удвоения числа ЗЭ и введения тактового генератора.

Для асинхронных потенциальных схем, использующих ЗЭ с двумя выходами, существует опасность неправильного срабатывания, связанная с не одновременностью установления сигналов на прямом и на инверсном выходе после перехода ЗЭ из одного состояния в другое. В результате этого в какой-то момент времени может оказаться, что некоторая переменная х и её инверсия принимают одинаковые значения. Проблема устранения источников возникновения подобных ситуаций называется проблемой риска.

Риск неправильного срабатывания имеет место лишь для тех ЗЭ, которые должны сохранять свое состояние в течение рассматриваемого такта. Если это состояние – “1”, то говорят о риске в единице, если – “0”, то о риске в нуле.

Рассмотрим в качестве примера функцию 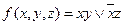. Для этого представления функции существует риск по переменной х. Функция f сохраняет значение “1” при изменении значения х, если y=1 и z=1, и сохраняет значение “0”, когда y=0, z=0. При одновременном обращении в “0” х и 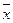выбранное представление функции f дает нулевое значение при любых y и z, в том числе и при z=y=1. Таким образом имеется риск в единице по переменной х. При других представлениях функции f, например 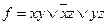, риск по х и по всем другим переменным отсутствует.

Справедливы следующие утверждения.

1. при представлении булевой функции произвольной ДНФ отсутствует риск в “0”, а при представлении произвольной КНФ отсутствует риск в “1”.

Для существующих х произвольную ДНФ функции f может представить в виде: 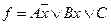, где А, В, С – булевые функции не зависящие от х. Если при каких-то фиксированных значениях всех переменных, отличных от х, функция f=0 как при x=0, так и при x=1, то это значит что A=В=С=0. Но тогда f=0 при 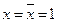так и при 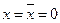. Таким образом риск в “0” по переменной х отсутствует. Однако остаётся возможность риска в “1”.

2. Представления булевой функции в виде СкДНФ и СкКНФ свободны от риска как в “0” так и в “1” по всем переменным. (Доказательство смотреть В.М.Глушков Синтез ЦА стр.356).

Таким образом при синтезе асинхронных потенциальных схем по соображениям надёжности иногда целесообразно отказаться от минимальных форм и пользоваться сокращенными.

Проблемы риска и гонок возникли лишь с появлением потенциальной элементной базы. Используемая ранее импульсно-потенциальная элементная база предусматривала применение статических триггеров со встроенной задержкой. При этом величина задержки была больше длительности импульсного сигнала поступающего на вход триггера. Таким образом переходные процессы формирования сигналов на выходах элементов памяти автомата начинались лишь после окончания входного импульсного сигнала и не оказывали воздействия на входы этих же элементов памяти по цепям обратной связи.