Проектирование КС на ПЗУ

(Краткая информация о ПЗУ и ППЗУ.)

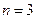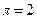Любое ПЗУ имеет n входов (адресных) и k выходов. Если , а , то ПЗУ содержит 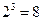ячеек памяти, в каждую из которых может быть записано слово длиной в 2 бита.

ПЗУ можно использовать не только для хранения информации, но и для ее обработки. Они могут быть использованы для реализации булевых функций, построения устройств управления различного назначения и т.д.

Рассмотрим проектирование КС на ПЗУ.

Пусть есть 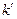булевых функций от 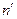переменных, представленных таблицами истинности. В ячейку памяти с нулевым адресом некоторого ПЗУ запишем значения функций из первой строки правой части таблицы истинности, в ячейку с адресом 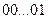- значения функций из второй строки таблицы истинности и т.д. Если теперь на адресные входы ПЗУ ( 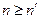; 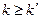) подать набор 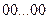, то на выходах ПЗУ появятся значения функций на наборе .

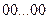Если 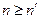, а 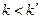, то для реализации системы булевой функций необходимо разбить её на подсистемы, каждая из которых содержит не более k функций и может быть реализована на одной схеме ПЗУ. Если 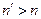, то могут быть использованы различные приёмы декомпозиции булевых функций по переменным, с реализацией получаемых подфункций на ПЗУ и последующим объединением выходов ПЗУ через различные элементы. Пусть существует система булевой функций 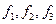от 4-х переменных, заданная таблицей истинности; её реализация на К155ПР6.

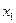
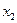
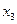
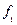
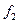
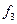
Более общий способ синтеза КС, реализующий булевы функции с применением ПЗУ и MUX, заключается в следующем.

Производят разложение булевых функций по k переменных, где k - число адресных входов MUX. Оставшиеся 2^k функций от (n-k) переменных реализуют, используя ПЗУ, после чего подключают выходы ПЗУ к входам данных MUX в соответствии с формулой разложения заданной функции. При этом дизъюнктивные члены разложения будут иметь вид:

,

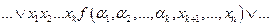где .

Пример:

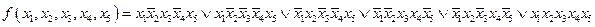э

Запишем f в виде:

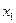
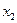
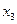
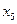
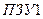
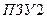
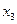
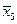
					1 х
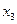
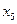
					х 1
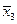
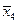
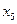
						1 1
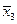
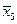
						1 х
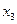
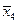
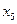
						х 1
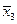
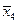
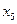
						1 1

Здесь число переменных 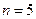. Используя MUX с двумя адресными входами и ПЗУ с тремя адресными входами и двумя выходами построим схему:

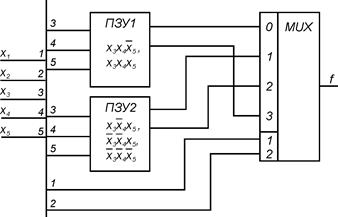
Схема реализации функции от пяти переменных.