Скалярный потенциал магнитного поля

В той части пространства, где плотность тока d равна нулю (правая часть уравнения (3.4) равна нулю), магнитное поле можно рассматривать как потенциальное и напряженность магнитного поля можно представить в виде

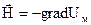, (3.5)

где U_м - скалярный потенциал магнитного поля.

В областях не занятых током (только для этих областей имеет смысл функция U_м) при постоянном значении магнитной проницаемости (m = const) скалярный потенциал магнитного поля подчиняется уравнению Лапласа:

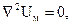
что вытекает из уравнений (3.2) и (3.5).

Линейный интеграл от напряженности магнитного поля по замкнутому контуру l, не охватывающему контура с током, равен нулю (закон полного тока). Поэтому (как в электростатическом поле), если условно принять равным нулю потенциал в некоторой точке Р (U_мр = 0), то разность потенциалов в точках А и Р будет равна потенциалу точки А:

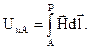
Однако, если выбрать такой путь интегрирования, который охватывает контур с током, правая часть уравнения (3.3) не будет равна нулю. Поэтому скалярный потенциал магнитного поля является функцией неоднозначной, но эта неоднозначность не оказывает влияния на расчет напряженности поля (i = const).

Разность магнитных потенциалов между двумя точками называют падением магнитного напряжения между этими точками.