Двумерные преобразования в однородных координатах

Как видно из приведенных выше формул двумерные преобразования имеют различный вид. Сдвиг реализуется сложением, а масштабирование и поворот - умножением. Это различие затрудняет формирование суммарного преобразования и устраняется использованием двумерных однородных координат точки, имеющих вид:

[ x y w]:

Здесь w - произвольный множитель не равный 0.

Двумерные декартовые координаты точки получаются из однородных делением на множитель w: X =x/w; Y =y/w

Однородные координаты можно представить как промасштабированные с коэффициентом w значения двумерных координат, расположенные в плоскости с Z =w. В силу произвольности значения w в однородных координатах не существует единственного представления точки, заданной в декартовых координатах.

Преобразования переноса, масштабирования и поворота в однородных координатах относительно центра координат все имеют одинаковую форму произведения вектора исходных координат на матрицу преобразования.

Для переноса

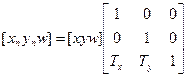-матрица переноса

Для масштабирования

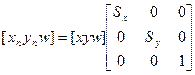
Для поворота

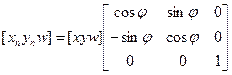
5. 3-х мерные преобразования. Суммарное преобразование. (км)

Аналогично тому, как двумерные преобразования описываются матрицами размером 3x3, трехмерные преобразования могут быть представлены в виде матриц размером 4x4. И тогда трехмерная точка (х, у, z) записывается в однородных координатах как (W*x, W*y, W*z, W), где W ≠0. Если W ≠1, для получения трехмерных-декартовых координат точки (х, у, z) первые три однородные координаты делятся на W. Отсюда, в частности, следует, что две точки H₁ и Н₂ в пространстве однородных координат описывают одну и ту же точку трехмерного пространства в том и только в том случае, когда H₁ =cH₂ для любой константы с, не равной нулю.

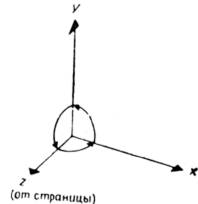Применяемая здесь трехмерная система координат является правосторонней

Перенос:

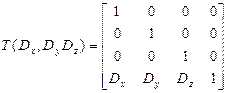
Масштабирование:

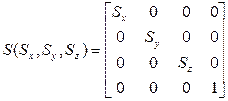
Поворот вокруг оси X:

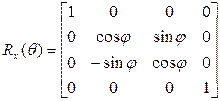
Поворот вокруг оси Y:

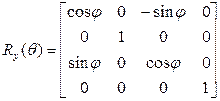
Поворот вокруг оси Z:

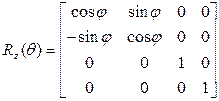
Столбцы (и строки) верхней левой подматрицы размером 3x3 матриц Rz, Rx и Ry представляют собой взаимно ортогональные единичные векторы, интерпретация которых такая же, что и в двумерном случае.

Все эти матрицы преобразований имеют обратные матрицы

обратная Т, получается подстановкой знака минус перед Dx, Dy и Dz,

обратная S — заменой Sx, Sy и Sz на обратные им значения,

а для каждой из трех матриц поворота — выбором отрицательного угла поворота

Результатом произвольной последовательности поворотов вокруг осей х, у и z является матрица А, имеющая вид:

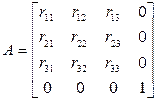
Подматрицу поворота размером 3x3 называют ортогональной, поскольку ее столбцы являются взаимно ортогональными единичными векторами. При повороте, задаваемом матрицей, эти единичные векторы совмещаются с осями х, у и z. Иногда возникает необходимость определить матрицу поворота, соответствующую таким направлениям. Матрицы поворота сохраняют длину и углы, а матрицы масштабирования и переноса не сохраняют.

Для любой ортогональной матрицы В обратная матрица совпадает с транспонированной B^-1=B^T. Этот результат является полезным, поскольку вычислять матрицу, обратную матрице поворота, приходится часто. В действительности для получения транспонированной матрицы не требуются даже взаимные пересылки между элементами массива, описывающего матрицу. Необходимо только при выборе элементов массива поменять местами индексы строк и столбцов. Отметим, что этот метод определения обратной матрицы дает тот же результат, что и способ обращения Rx, Ry, Rz, основанный на подстановке

знака минус перед углом φ/

Можно перемножить произвольное число матриц поворота, масштабирования и переноса. Результат всегда будет иметь вид

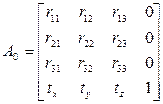
Рисование в Windows:

6. GDI. Контекст устройства.(км)

Графические функции из состава WinAPI объединяются в отдельную группу – подсистему GDI.

GDI (Grafic device interface)- можно представить себе как графическую машину, которая исп. Windows и ее приложения ,для отображения и манипулирования графикой, причем эти функции не зависят от используемого устройства.

Приложение --> GDI --> драйвер устройства --> видеопамять

Аппаратная независимость реализуется через использование драйверов устройств, которые переводят функции GDI в команды, воспроизводимые устройством вывода.