NGP – Network Graphic Protocol

Первые результаты по стандартизации были получены применительно к сети ARPA в рамках работ по разработке протоколов для аппаратно и машинно-независимого представления графических данных в сети.

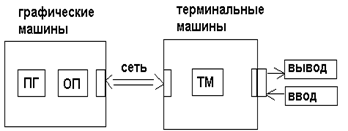
ПГ - Прикладная Программа

ОП - обслуживающая программа

ТМ - терминальная программа

Международная деятельность по стандартизации машинной графики

1976г. – были сформулированы и обсуждены задачи стандартизации. Комитет по стандартизации машинной графики (GSPC) ACM/3IGGRAPH

Стандарт Core-system (GSPC - 77)

1) Разделение функций ввода вывода

2) Минимизация отличий выводов

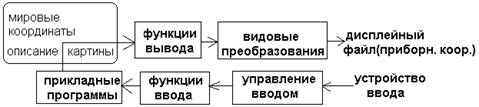
3) Концепция 2х координатных систем (мировой и приборной системы координат)

4) Концепция дисплейного файла, содержащего приборную координатную информацию (контекст)

5) Обеспечение функций преобразования данных из мировой системы в приборную путем вызова видового преобразования

Матричные

операции:

4. 2-мерные преобразования в декартовых и однородных координатах. (км)

XYZ – обыкновенные декартовы координаты

xyz – однородные координаты

Видовые преобразования:

1) перенос

2) поворот

3) масштабирование

X_n=X+T_x

Y_n=Y+T_y

P_n=P+T

p=[x,y] – вектор одномерной матрицы

p – вектор координат

P_n – в вектор новых координат

T – вектор

Масштабирование

X_n=X*S_x

Y_n=Y*S_y

P_n=P*S

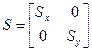- матрица и масштабирование

Поворот

X_n=X*cosφ – Y*sinφ

Y_n= X*sinφ – Y* cosφ

P_n=P*R

φ-угол поворота

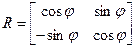
Столбцы и строки матрицы поворота представляют собой взаимно ортогональные единичные векторы. В самом деле квадраты длин векторов-строк равны единице:

cosφ * cosφ + sinφ * sinφ = 1

- sinφ * (- sinφ) + cosφ * cosφ = 1

а скалярное произведение векторов-строк есть cosφ(-sin) + sinφ*cosφ = 0

Так как скалярное произведение векторов А * В = |А| * |В| * cosφ где |A| - длина вектора А, |В| - длина вектора В, а φ - наименьший положительный угол между ними, то из равенства 0 скалярного произведения двух векторов-строк длины 1 следует, что угол между ними равен 90.