Разрешение конфликтов: открытое хеширование
Пусть имеется n элементов а1, а2, а3, . . ., аn , на основе которых требуется построить хеш-таблицу, причем некоторые ключи могут конфликтовать между собой, претендуя на одну и ту же ячейку таблицы. Идея открытого хеширования совершенно прозрачна: связать все элементы с одним и тем же значением хеш-функции во вспомогательный линейный список. Данный метод иногда называют методом цепочек.
Обращаю внимание, что мы еще раз приходим к необходимости использования комбинированной структуры данных – массива указателей. Хеш-таблица как массив записей должна хранить не только ключи элементов, но и по два указателя на начало и конец вспомогательного списка.
| индекс | ключ |
| ||||||
| аi h(аi)=1 |    начало начало
| |||||||
  конец конец
| ||||||||
 nil nil
| ||||||||
| nil | ||||||||
| аs h(аs)=3 | nil | |||||||
| nil | ||||||||
| аk h(аk)=4 |
 начало начало
| |||||||
 конец конец
| ||||||||
| . . . . . | . . . . | |||||||
| m | nil | |||||||
| nil |
Алгоритм построения хеш-таблицы:
· находим значение хеш-функции для очередного ключа и по этому значению как индексу входим в таблицу
· если данная клетка таблицы пустая, то записываем в нее соответствующий ключ
· если ячейка занята, то сравниваем хранящийся там ключ с заданным ключом:
o если ключи совпадают, то каким-то образом обрабатываем повторный ключ (например, просто ничего не выполняем)
o если ключи не совпадают, то добавляем новый ключ в конец списка
Алгоритм поиска в построенной таблице:
· находим значение хеш-функции для искомого ключа и по этому значению как индексу входим в таблицу
· если ячейка с найденным индексом пустая, то поиск заканчивается неудачей
· если ячейка не пустая, то выполняем сравнение ключей:
o если ключи совпадают, то поиск заканчивается за одно сравнение
o если ключи не совпадают, то организуем просмотр линейного вспомогательного списка с положительным или отрицательным результатом
Пример. Задано 10 целочисленных ключей, на основе которых надо построить хеш-таблицу размерности 5, используя для разрешения конфликтов метод открытого хеширования. Поскольку число исходных элементов n=10 больше размерности таблицы (m=5), то без использования вспомогательных списков таблицу построить нельзя. Набор входных ключей с соответствующими значениями хеш-функции приведены в следующей таблице (использована простейшая хеш-функция):
| ключ | ||||||||||
| значение хеш-функции |
Тогда хеш-таблица будет иметь следующий вид:
| индекс | ключ | указатели | ||||||
| nil | ||||||||
| nil | ||||||||
| nil | ||||||||
| ||||||||
  начало начало
| ||||||||
  конец конец
| ||||||||
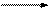
| ||||||||
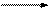 конец конец
| ||||||||
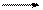 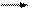 
| ||||||||
  конец конец
|
Подсчитаем для данного примера среднее число сравнений, которые необходимо сделать для поиска любого из 10 исходных ключей:
· ключ 33 – одно сравнение, т.к. он непосредственно находится в ячейке таблицы
· ключи 17 и 09 – тоже по одному сравнению
· ключ 04 – два сравнения (в ячейке 5 находится ключ 09, идем по списку, совпадение на первом элементе)
· ключ 22 – 2 сравнения
· ключи 19 и 42 – по 3 сравнения (вторые элементы в списках)
· ключ 53 – 2 сравнения
· ключ 64 – 4 сравнения
· ключ 25 – 1 сравнение
Итого – 20 сравнений, т.е. в среднем 2 сравнения на один ключ.
Из примера видно, что для данного метода большое значение имеет равномерность распределения ключей по хеш-таблице, что гарантирует короткие вспомогательные списки и тем самым уменьшает число сравнений при поиске. Наихудшим является случай, когда для всех ключей хеш-функция дает одно и тоже значение, и все элементы выстраиваются в один длинный линейный список.
Другим фактором, влияющим на эффективность открытого хеширования, является размер хеш-таблицы по отношению к числу входных данных. Если эти величины равны, то теоретически можно обойтись без линейных списков, если между ключами нет конфликтов. На практике рекомендуют выбирать размер хеш-таблицы равным n/2.
Дата добавления: 2020-07-18; просмотров: 586;











