Function lagr(x As Double, xe As Variant, ye As Variant)

n = Application.Count(xe)

lagr = 0

For i = 1 To n

p = 1

For j = 1 To n

If j <> i Then p = p * (x - xe(j)) / (xe(i) - xe(j))

Next j

lagr = lagr + ye(i) * p

Next i

End Function

Function Newtonn(x As Double, xe As Variant, ye As Variant)

n = Application.Count(xe)

Dim D() As Variant

ReDim D(n, n) As Variant

‘конечные разности 1-ого порядка в 1-0м столбце массива d

For i = 1 To n - 1

D(i, 1) = ye(i + 1) - ye(i)

Next i

For j = 2 To n - 1

For i = 1 To j

D(i, j) = D(i + 1, j - 1) - D(i, j - 1)

Next i

h = xe(2) - xe(1)

Next j

ne = ye(1)

For i = 1 To n - 1

p = 1

For j = 1 To i

p = p * (x - xe(j)) / (j * h)

Next j

ne = ne + p * D(1, i)

Next i

Newtonn = ne

End Function

Некоторые комментарии к программам:

модули

– Function lagr(x As Double, xe As Variant, ye As Variant)

– Function Newtonn(x As Double, xe As Variant, ye As Variant)

– Sub Kanon3(x As Double, xe As Variant, ye As Variant, Polinom As String, Kanon_znac As Double)

обеспечивают вычисления значений интерполяционных полиномов Лагранжа, Ньютона и канонического интерполяционного полинома.

Подпрограмма Private Sub CommandButton3_Click()обеспечивает ввод исходных данных и отображение их в объекте Label5.

ПодпрограммаPrivate Sub CommandButton4_Click()обеспечивает вызов модулей lagr, Newtonn и Kanon3.

При этом модуль Kanon3 выполнен не в виде функции Function, а в виде подпрограммы Sub. Такая организация позволяет получать из подпрограммы Kanon3 несколько выходных параметров, в частности параметр Polinom As String и параметр Kanon_znac As Double.

Калькулятор поддерживает вычисление значений интерполяционных полиномов степенью не выше пятой, хотя изменения программы для увеличения степени вычисляемых интерполяционных полиномов достаточно просты.

Если в качестве исходной интерполяционной таблицы ввести значения X = 1,4, 5, 7и Y = 3, 10, 2, 5 и вычислить значение интерполяционного полинома для X = 2.372, то получим результаты, показанные на рис. 3.4.10.

Значения канонического интерполяционного полинома и полинома Лагранжа для X = 2.372 совпадают и равны величине 17.597. В то время как значение интерполяционного полинома Ньютона для X = 2.372равно величине 9.005. Дело в том, в калькуляторе для вычисления значений интерполяционного полинома Ньютона используется формула для равноотстоящих узлов интерполяционной таблицы, а это условие в рассматриваемом примере не соблюдается.

Так что для введённой интерполяционной таблицы аналитическое выражение интерполяционного полинома имеет вид P₃(x) = -28.83 + 43.04 x – 12.17 x² + 0.96 x³, а его значение при X = 2.372 равно величине 17.597

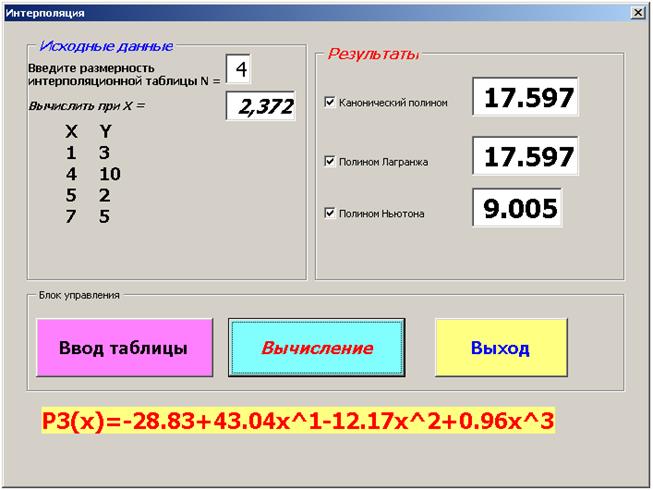
Рис. 3.4.10